Llei d’Ohm. Impedància#
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
Llei d’Ohm a AC#
Si nosaltres volem mantenir la nsotra preuada llei d’Ohm a AC, haurem de canviar la resistència per quelcom que reprodueixi el canvis de fase de la intensitat respecte al voltatge. La impedància complexa \(Z\) és la solució:
\(\Large I = \frac{U}{Z}\)
Impedància d’una resistència#
La resistència no ens va donar problemes
\(Z = R\)
Impedància d’un condensador#
El condensador va introduir un avançament de la intensitat. Per altra banda es pot comprovar que la intensitat aumenta amb la freqüència i és proporcional a la capacitat del condensdor. Per tant, tenent en compte que la intensitat és inversament proporcional a la impedància
\(\large Z \equiv X_C = -j \ \frac{1}{C\omega}\)
La impedància d’un condensador s’anomena reactància capacitiva.
Impedància d’una bobina#
La bobina o inductor va introduir un retard de la intensitat. Per altra banda es pot comprovar que la intensitat disminueix amb la freqüència i és inversament proporcional a la inductància \(L\), que s’expressa en henrys (H). Per tant, tenent en compte que la intensitat és inversament proporcional a la impedància
\(\large Z \equiv X_L = j \ L\)
La impedància d’un inductor s’anomena reactància inductiva.
Associacions d’impedàncies#
Les fòrmules d’associació sèrie i paral·lel de resistències són vàlides per les impedàncies (compte! treballem amb nombres complexos)
Associació en sèrie#
\(Z_s = \sum Z_i\)
Associació en paral·lel#
\(\large \frac{1}{Z_p} = \sum \frac{1}{Z_i}\)
Associació en sèrie. Triangle d’impedàncies#
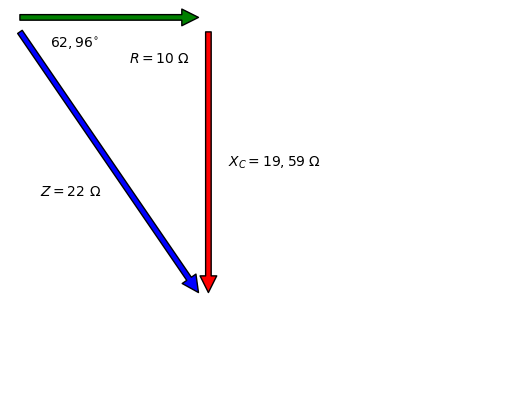
Ja hem dit que treballem amb impedàncies complexes. Qaun sumem dos elements en sèrie, per exemple una resistència i un condensador, hem de fer uina suma vectorial. R, \(X_C\) i Z formen un triangle, anomenat triangle d’impedàncies.
Veiem un exemple:
Un circuit sèrie amb una resistència \(R = 10 \ \Omega\) i un condensador \(C = 162,48 \ \mu F\) està connectat a una xarxa monofàsica \(U = 200 V\) i \(f = 50 Hz\)
import numpy as np
import matplotlib.pyplot as plt
R = 10
C = 162.48 * 10**(-6)
U = 220
f = 50
w = 2 * np.pi * f
Xc = 0 -1j/(C*w)
Xc
-19.590711852769j
\(X_{C} = 19.59_{-90^{\circ}} \ \Omega\)
Z = R + Xc
Z
(10-19.590711852769j)
modZ = np.abs(Z)
modZ
21.995362940816044
angZ = np.degrees(np.angle(Z))
angZ
-62.958143957668284
\(Z = 22_{-62,96^{\circ}} \ \Omega\)
Representem aquesta suma vectorial i visualitzarem el triangle d’impedàncies:
Show code cell source
%matplotlib inline
plt.annotate('', xy=(np.real(Z), np.imag(Z)), xytext=(0, 0),
arrowprops=dict(facecolor='blue', shrink=0.05),
)
plt.annotate('', xy=(np.real(Z), 0), xytext=(0, 0),
arrowprops=dict(facecolor='green', shrink=0.05),
)
plt.annotate('', xy=(np.real(Z), np.imag(Z)), xytext=(np.real(Z), 0),
arrowprops=dict(facecolor='red', shrink=0.05),
)
plt.annotate("$Z = 22 \ \Omega$", xy=(1.5, -12))
plt.annotate("$R = 10 \ \Omega$", xy=(6, -3))
plt.annotate("$X_{C} = 19,59 \ \Omega$", xy=(11,-10))
plt.annotate("$62,96^{\circ}$", xy=(2,-2))
plt.xlim(0, 25)
plt.ylim(-25, 0)
plt.axis('off')
plt.show()