Comparació propietats dels metalls#
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# Dades de la Wikipèdia, excepte Límit elàstic, Resistència al trencament i Allargament.
# Buscant una font més fiable que el llibre de McGraw-Hill, està ple d'errades
df = pd.DataFrame({
'Nom':['Cu','Al','Mg','Ti','Pb','Sn','Zn','Ni','Fe'],
# densitat ρ [10³·kg/m³]
'Densitat':[8.96,2.70,1.738,4.506,11.34,7.365,7.14,8.908,7.874],
# punt de fusió [⁰C]
'Punt de fusió':[1084.62,660.32,650,1670,327.46,231.93,419.53,1455,1538],
# conductivitat tèrmica ϰ [W/m·⁰C]
'Conductivitat tèrmica':[401,237,156,21.9,35.3,66.8,116,90.9,80.4],
# Dilatació tèrmica λ [10⁻⁶·K⁻¹]
'Dilatació tèrmica':[16.5,23.1,24.8,8.6,28.9,22,30.2,13.4,11.8],
# mòdul elàstic E [GPa]
'Mòdul elàstic':[110,70,45,116,16,50,108,200,211],
# límit elàstic σe [MPa]
'Límit elàstic':[69,17,41,240,3.5,2.55,7,138,130],
# Resistència al trencament R [MPa]
'Resistència al trencament':[220,55,165,330,19.6,34.3,117,483,260],
# Allargament ε [%]
'Allargament':[45,25,6,30,50,40,32,40,45],
# Duresa HB [MPa]
'Duresa':[874,245,260,716,38.3,350,412,700,490],
# Resistivitat elèctrica [10⁻⁹·Ω·m]
'Resistivitat':[16.78,28.2,43.9,420,208,115,59,69.3,96.1]
})
df
| Nom | Densitat | Punt de fusió | Conductivitat tèrmica | Dilatació tèrmica | Mòdul elàstic | Límit elàstic | Resistència al trencament | Allargament | Duresa | Resistivitat | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Cu | 8.960 | 1084.62 | 401.0 | 16.5 | 110 | 69.00 | 220.0 | 45 | 874.0 | 16.78 |
| 1 | Al | 2.700 | 660.32 | 237.0 | 23.1 | 70 | 17.00 | 55.0 | 25 | 245.0 | 28.20 |
| 2 | Mg | 1.738 | 650.00 | 156.0 | 24.8 | 45 | 41.00 | 165.0 | 6 | 260.0 | 43.90 |
| 3 | Ti | 4.506 | 1670.00 | 21.9 | 8.6 | 116 | 240.00 | 330.0 | 30 | 716.0 | 420.00 |
| 4 | Pb | 11.340 | 327.46 | 35.3 | 28.9 | 16 | 3.50 | 19.6 | 50 | 38.3 | 208.00 |
| 5 | Sn | 7.365 | 231.93 | 66.8 | 22.0 | 50 | 2.55 | 34.3 | 40 | 350.0 | 115.00 |
| 6 | Zn | 7.140 | 419.53 | 116.0 | 30.2 | 108 | 7.00 | 117.0 | 32 | 412.0 | 59.00 |
| 7 | Ni | 8.908 | 1455.00 | 90.9 | 13.4 | 200 | 138.00 | 483.0 | 40 | 700.0 | 69.30 |
| 8 | Fe | 7.874 | 1538.00 | 80.4 | 11.8 | 211 | 130.00 | 260.0 | 45 | 490.0 | 96.10 |
Densitat#
df.plot(kind='bar',x='Nom',y='Densitat')
plt.ylabel('ρ [10³·kg/m³]')
Text(0, 0.5, 'ρ [10³·kg/m³]')
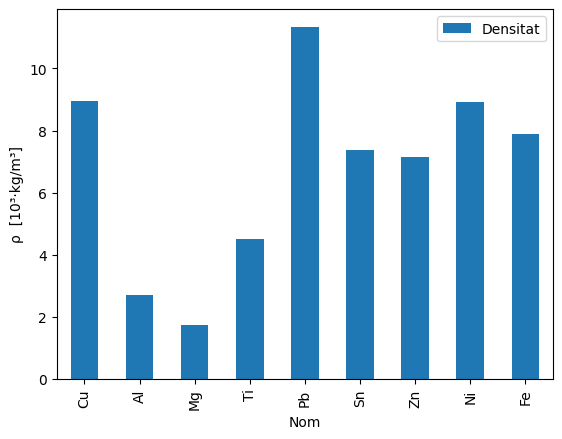
Fixeu-vos en la baixa densitat de l’alumni i el magnesi. Els aliatges de l’alumini reben el nom d”aliatges lleugers, i els de magnesi d”aliatges ultralleugers.
Per altra banda fixeu-vos l’alta densitat del plom. D’aquí el seu ús a projectils, llastres per bussos o plomades.
Temperatura de fusió#
df.plot(kind='bar',x='Nom',y='Punt de fusió')
plt.ylabel('Tf [⁰C]')
Text(0, 0.5, 'Tf [⁰C]')
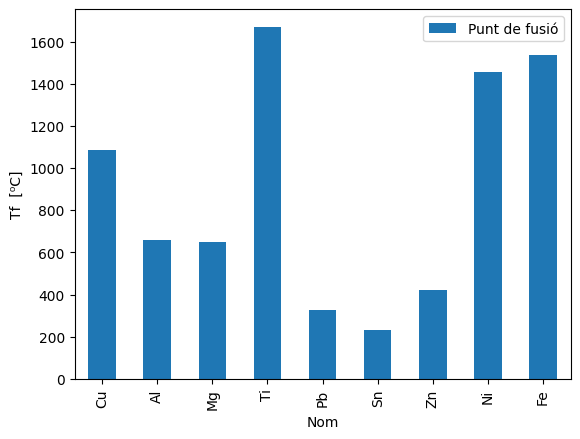
La baixa temperatura de fusió de l’estany i el plom justifiquen el seu ús a soldadures i fusibles.
Conductivitat tèrmica#
df.plot(kind='bar',x='Nom',y='Conductivitat tèrmica')
plt.ylabel('ϰ [W/m·⁰C]')
Text(0, 0.5, 'ϰ [W/m·⁰C]')
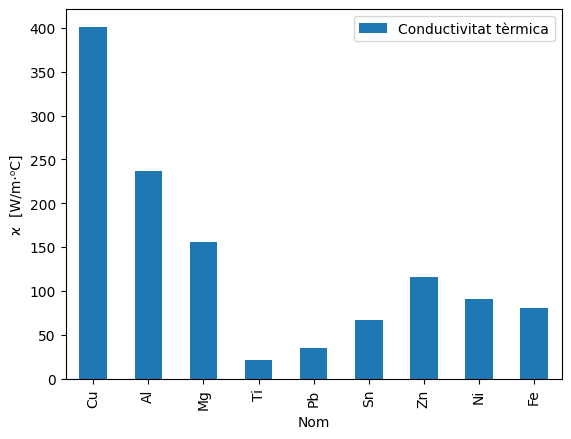
L’alta conductivitat tèrmica del coure justifica el seu ús a recipients per a cuinar aliments.
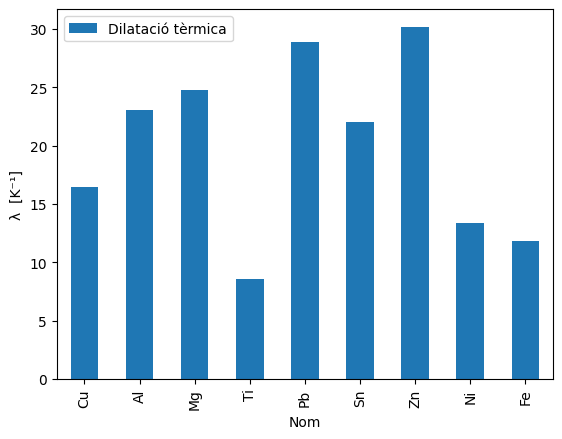
Dilatació tèrmica#
df.plot(kind='bar',x='Nom',y='Dilatació tèrmica')
plt.ylabel('λ [K⁻¹]')
Text(0, 0.5, 'λ [K⁻¹]')
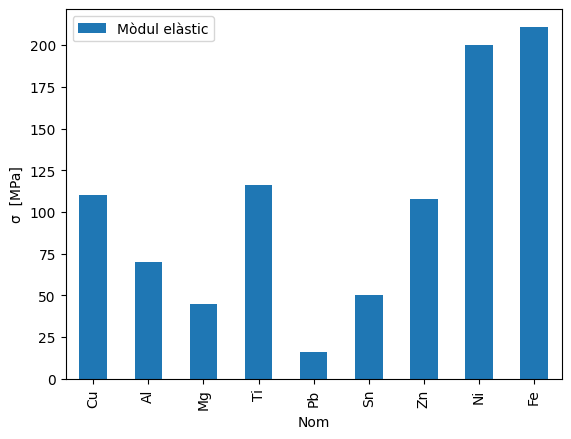
Mòdul elàstic#
df.plot(kind='bar',x='Nom',y='Mòdul elàstic')
plt.ylabel('σ [MPa]')
Text(0, 0.5, 'σ [MPa]')
Límit elàstic#
df.plot(kind='bar',x='Nom',y='Límit elàstic')
plt.ylabel('σe [MPa]')
Text(0, 0.5, 'σe [MPa]')
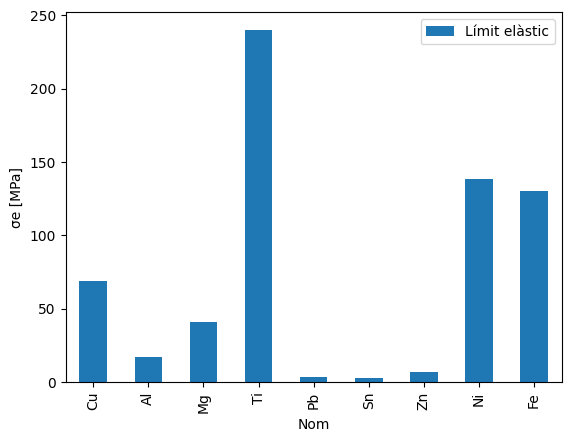
El límit elàstic del titani, juntament amb la seva baixa densitat, justifiquen el seu ús a estructures aeroespacials, ulleres …
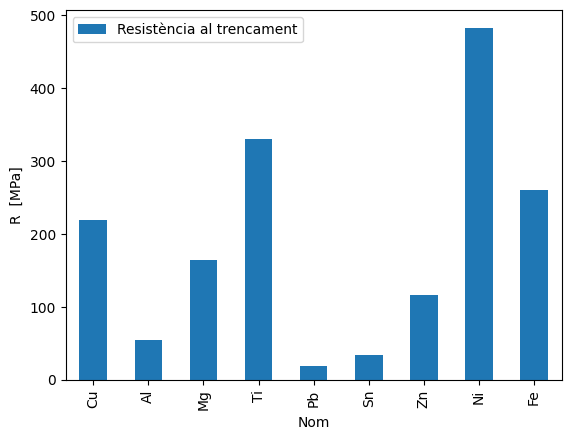
Resistència al trencament#
df.plot(kind='bar',x='Nom',y='Resistència al trencament')
plt.ylabel('R [MPa]')
Text(0, 0.5, 'R [MPa]')
Allargament#
df.plot(kind='bar',x='Nom',y='Allargament')
plt.ylabel('ε [%]')
Text(0, 0.5, 'ε [%]')
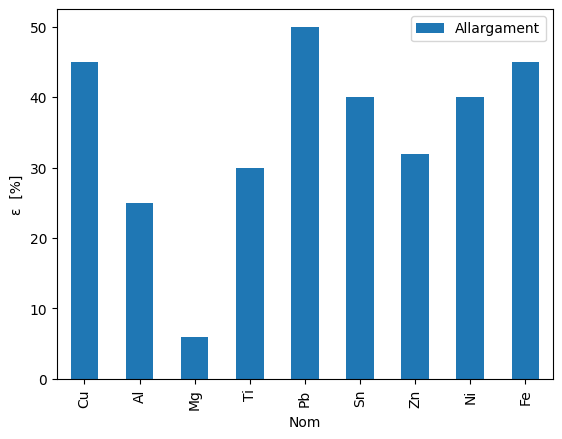
Molts d’aquest metalls són molt dúctils, degut a la possibilitat d’una alta deformàció plàstica
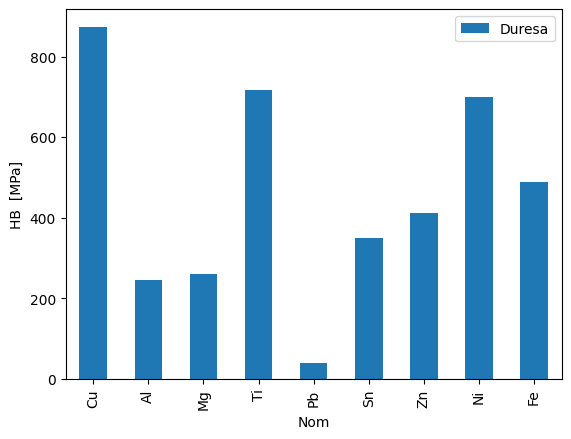
Duresa#
df.plot(kind='bar',x='Nom',y='Duresa')
plt.ylabel('HB [MPa]')
Text(0, 0.5, 'HB [MPa]')
Resistivitat elèctrica#
df.plot(kind='bar',x='Nom',y='Resistivitat')
plt.ylabel('ρ [10⁻⁹·Ω·m]')
Text(0, 0.5, 'ρ [10⁻⁹·Ω·m]')
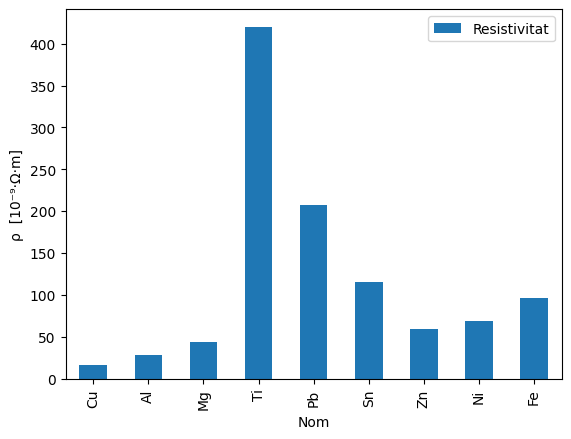
La baixa resistivitat del coure i l’alumini, juntament amb la seva ductibilitat, justifiquen el seu ús a cables elèctrics. L’alumini és molt més lleuger, per això s’utilitza a xarxes d’alta tensió, alleugerant la càrrega de l’estructura de la torre.
Efecte de la densitat en la propietat#
Relació resistència mecànica / pes#
rho=df['Densitat']
df["Relació Resistència/pes"]= df["Límit elàstic"].div(other = rho)
df
| Nom | Densitat | Punt de fusió | Conductivitat tèrmica | Dilatació tèrmica | Mòdul elàstic | Límit elàstic | Resistència al trencament | Allargament | Duresa | Resistivitat | Relació Resistència/pes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Cu | 8.960 | 1084.62 | 401.0 | 16.5 | 110 | 69.00 | 220.0 | 45 | 874.0 | 16.78 | 7.700893 |
| 1 | Al | 2.700 | 660.32 | 237.0 | 23.1 | 70 | 17.00 | 55.0 | 25 | 245.0 | 28.20 | 6.296296 |
| 2 | Mg | 1.738 | 650.00 | 156.0 | 24.8 | 45 | 41.00 | 165.0 | 6 | 260.0 | 43.90 | 23.590334 |
| 3 | Ti | 4.506 | 1670.00 | 21.9 | 8.6 | 116 | 240.00 | 330.0 | 30 | 716.0 | 420.00 | 53.262317 |
| 4 | Pb | 11.340 | 327.46 | 35.3 | 28.9 | 16 | 3.50 | 19.6 | 50 | 38.3 | 208.00 | 0.308642 |
| 5 | Sn | 7.365 | 231.93 | 66.8 | 22.0 | 50 | 2.55 | 34.3 | 40 | 350.0 | 115.00 | 0.346232 |
| 6 | Zn | 7.140 | 419.53 | 116.0 | 30.2 | 108 | 7.00 | 117.0 | 32 | 412.0 | 59.00 | 0.980392 |
| 7 | Ni | 8.908 | 1455.00 | 90.9 | 13.4 | 200 | 138.00 | 483.0 | 40 | 700.0 | 69.30 | 15.491693 |
| 8 | Fe | 7.874 | 1538.00 | 80.4 | 11.8 | 211 | 130.00 | 260.0 | 45 | 490.0 | 96.10 | 16.510033 |
El titani és el que presenta de llarg la millor característica, com ja comentaven abans.
Producte resistivitat·densitat#
df["Producte Resistivitat·densitat"]= df["Resistivitat"].mul(other = rho)
df
| Nom | Densitat | Punt de fusió | Conductivitat tèrmica | Dilatació tèrmica | Mòdul elàstic | Límit elàstic | Resistència al trencament | Allargament | Duresa | Resistivitat | Relació Resistència/pes | Producte Resistivitat·densitat | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Cu | 8.960 | 1084.62 | 401.0 | 16.5 | 110 | 69.00 | 220.0 | 45 | 874.0 | 16.78 | 7.700893 | 150.3488 |
| 1 | Al | 2.700 | 660.32 | 237.0 | 23.1 | 70 | 17.00 | 55.0 | 25 | 245.0 | 28.20 | 6.296296 | 76.1400 |
| 2 | Mg | 1.738 | 650.00 | 156.0 | 24.8 | 45 | 41.00 | 165.0 | 6 | 260.0 | 43.90 | 23.590334 | 76.2982 |
| 3 | Ti | 4.506 | 1670.00 | 21.9 | 8.6 | 116 | 240.00 | 330.0 | 30 | 716.0 | 420.00 | 53.262317 | 1892.5200 |
| 4 | Pb | 11.340 | 327.46 | 35.3 | 28.9 | 16 | 3.50 | 19.6 | 50 | 38.3 | 208.00 | 0.308642 | 2358.7200 |
| 5 | Sn | 7.365 | 231.93 | 66.8 | 22.0 | 50 | 2.55 | 34.3 | 40 | 350.0 | 115.00 | 0.346232 | 846.9750 |
| 6 | Zn | 7.140 | 419.53 | 116.0 | 30.2 | 108 | 7.00 | 117.0 | 32 | 412.0 | 59.00 | 0.980392 | 421.2600 |
| 7 | Ni | 8.908 | 1455.00 | 90.9 | 13.4 | 200 | 138.00 | 483.0 | 40 | 700.0 | 69.30 | 15.491693 | 617.3244 |
| 8 | Fe | 7.874 | 1538.00 | 80.4 | 11.8 | 211 | 130.00 | 260.0 | 45 | 490.0 | 96.10 | 16.510033 | 756.6914 |
Per a un cable de resistència \(R\), llargada \(L\) i secció fixades, la massa del cable té l’expressió, en funció de la resistivitat \(\rho\) i densitat \(d\) del material amb que està fet:
\(M = \frac{\rho}{R} · L^2·d\)
Per tant, quan més baix el producte \(\rho · d\) més lleuger el cable i menys esforç ha de suportar l’estructura que manté elevat el cable. Com veieu, l’alumni és millor candidat que el coure en aquest cas.