Exercicis resolts 1/2

PAU 2000 S6 4B

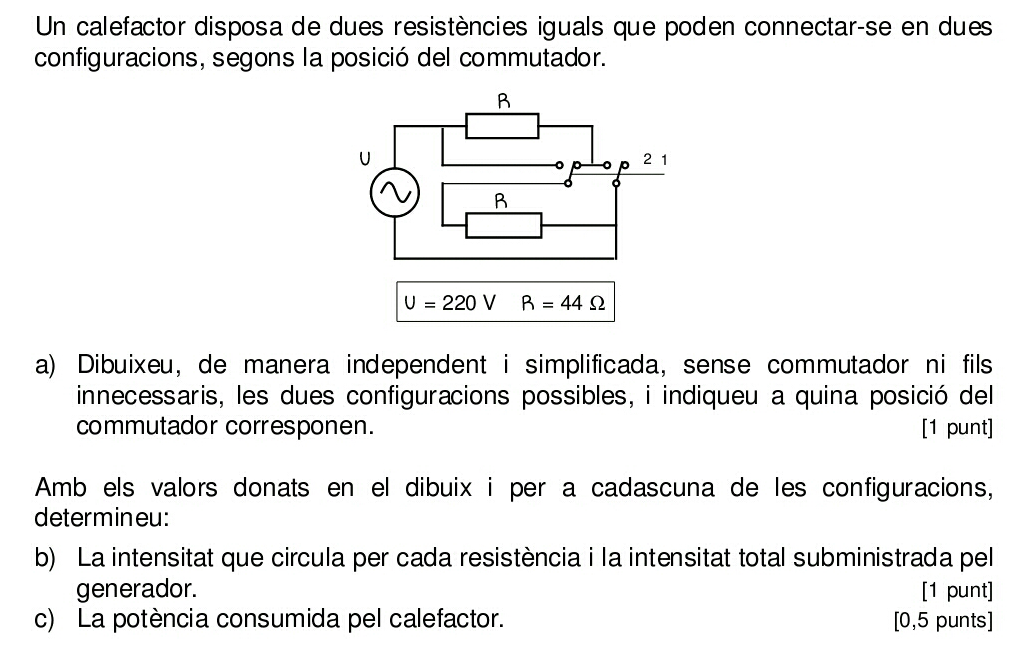
a)

posició 1:

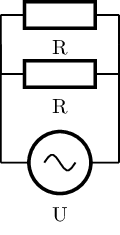
posició 2:

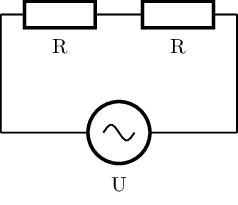
b)

posició 1:

Resistències en paral·lel

\(R_p = (\frac{1}{R} + \frac{1}{R})^{-1} = (\frac{2}{R})^{-1} = \frac{R}{2}\)

\( I_{tot} = \frac{U}{R_p} \)

Rp = 44/2
U = 220
Itot = U/Rp
Itot

10.0

Es a dir, en total 10A subministrats pel generador, 5A circulen per cada resistència

posició 2:

Resistències en sèrie

\(R_s = R + R = 2R\)

\( I_{tot} = \frac{U}{R_s} \)

Rs = 2 * 44
U = 220
Itot = U/Rs
Itot

2.5

Es a dir 2,5A subministrats pel generador, que passen per les dues resistències

c)

\(P = U \cdot I_{tot}\)

posició 1:

P = 220 * 10
P

2200

2200 W consumits pel calefactor

posició 2:

P = 220 * 2.5
P

550.0

550 W consumits pel calefactor

PAU 2005 S3 3B

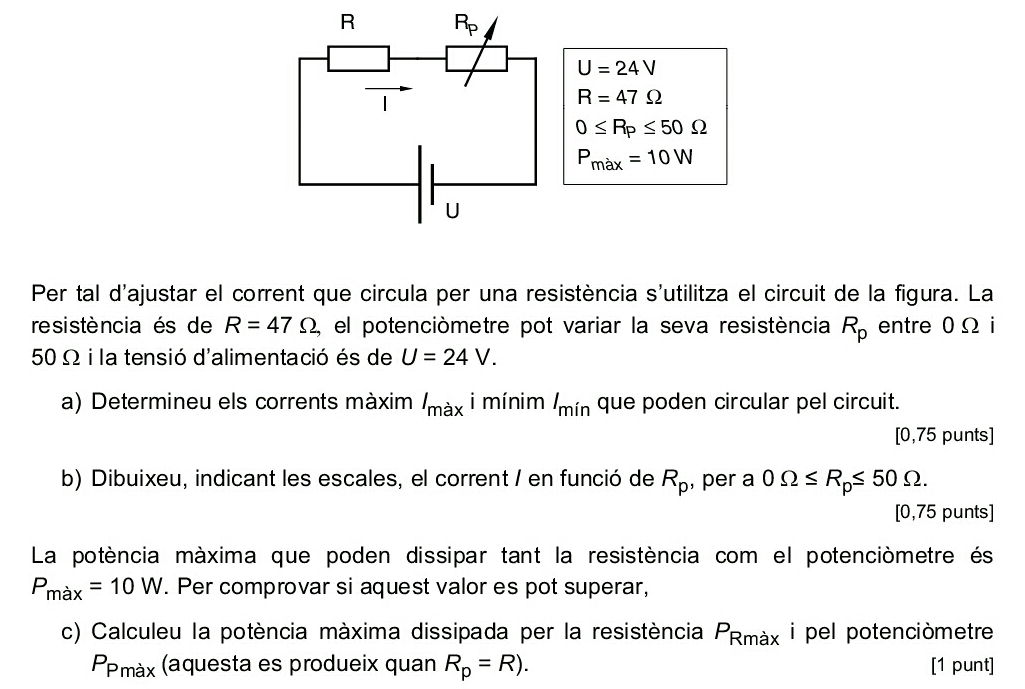
\(R_{tot} = R + R_p \Rightarrow R_{mín} = 47\Omega + 0\Omega = 47\Omega, R_{màx} = 47\Omega + 50\Omega = 97\Omega\)

\(I = \frac{U}{R_{tot}} \Rightarrow I_{màx} = \frac{U}{R_{min}}, I_{min} = \frac{U}{R_{màx}}\)

U = 24
Rmin = 47
Imax = U/Rmin
Imax

0.5106382978723404

U = 24
Rmax = 97
Imin = U/Rmax
Imin

0.24742268041237114

Per tant \(I{màx} = 510,6 mA\) i \(I{mín} = 247,4 mA\)

b)

import matplotlib.pyplot as plt
import numpy as np
U = 24
x = np.linspace(0, 50, 100)
plt.plot(x, U/(47+x)) 
plt.xlabel('$R_p [ \Omega ]$')
plt.ylabel('I [A]')
plt.title("Intensitat")
plt.show();

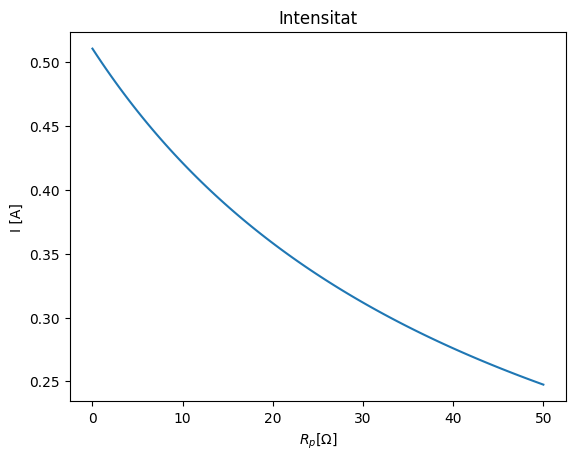
c)

\(PR = I^2 \cdot R = (\frac{U}{R+R_p})^2 \cdot R\)

\(PR_{màx} \Rightarrow R_p = 0 \Rightarrow PR_{màx} = \frac{U^2}{R}\)

PRmax = U**2/47
PRmax

12.25531914893617

Per tant la resistència R pot arribar a generar 12,25W, més dels 10W que pot dissipar

\(PR_p = I^2 \cdot R_p = (\frac{U}{R+R_p})^2 \cdot R_p\)

\(PR_{p,màx} \Rightarrow R_p = R \Rightarrow PR_{màx} = \frac{U^2}{4R}\)

PRPmax = U**2/(4*47)
PRPmax

3.0638297872340425

En canvi el potenciòmetre generarà com a màxim 3,063W, per sota del 10W que pot dissipar

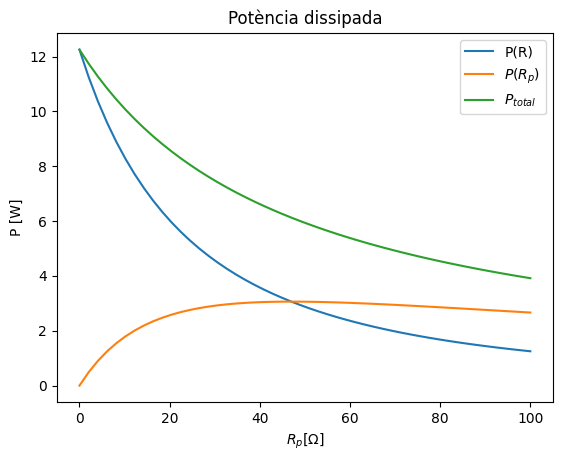
Veiem gràficament el comportament:

import matplotlib.pyplot as plt
import numpy as np
U = 24
x = np.linspace(0, 100, 50)
plt.plot(x, 47*(U/(47+x))**2, label='P(R)')
plt.plot(x, x*(U/(47+x))**2, label='$P(R_p)$')
plt.plot(x, 47*(U/(47+x))**2+x*(U/(47+x))**2, label='$P_{total}$')
plt.xlabel('$R_p [ \Omega ]$')
plt.ylabel('P [W]')
plt.title("Potència dissipada")
plt.legend();
plt.show();