Dinàmica de les rotacions#
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
A física heu estudiat el moviment d’una partícula, i les lleis de Newton associades. Però, que passa quan parlem de rotacions d’un cos? La dinàmica de les rotacions, del cos rígid, és un nou problema per a vosaltres.
Parell de forces o moment#
Quan empenyem una porta, per a una mateuixa força, és més efectiu si empenyeu el més lluny possible de les frontisses. Mai us heu trobat que us costa obrir la porta de l’ascensor quan empenyeu pel costat de les frontisses?
Per altra banda, l’efecte és més efectiu si empenyeu perpendicularment a la porta. De fet, l’eficiència va relacionada amb un factor \(sin(\varphi)\). Penseu en un molinet de vent, que gira més ràpid encarat al vent.
Naturalment girarà més quan empenyem amb més força.
Tot això ho podem expressar matemàticament amb
\(\Gamma = r \cdot F \cdot sin(\varphi)\)
Aquesta expressió correspon a l’àlgebra vectorial al mòdul del producte vectorial dels vectors \(\overrightarrow{r}\) i \(\overrightarrow{F}\)
El producte vectorial es representa pel símbol \(\times\) o amb el símbol \(\wedge\)
\(\overrightarrow{\Gamma} = \overrightarrow{r} \times \overrightarrow{F}\)
\(\Gamma\) és el parell o moment de la força \(\overrightarrow{F}\) a la distància \(\overrightarrow{r}\), un vector perpendicular a \(\overrightarrow{r}\) i a \(\overrightarrow{F}\), i amb el sentit de l’avanç d’un cargol girant de \(\overrightarrow{r}\) cap a \(\overrightarrow{F}\) amb els dos vectors units al seu origen, o el que és el mateix, avançant \(\overrightarrow{F}\) amb el seu origen lligat a \(\overrightarrow{r}\). Es representa amb la lletra grega gamma majúscula \(\overrightarrow{\Gamma}\) o amb la letra M majúscula \(\overrightarrow{M}\).
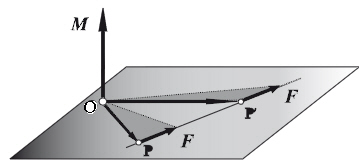
El mòdul del moment val dos vegades l’àrea del triangle definit per \(\overrightarrow{r}\) i \(\overrightarrow{F}\), i no varia si desplacem la força \(\overrightarrow{F}\) al llarg de la seva línea d’acció. Una tècnica habitual per calcular moments és fer servir aquesta propietat i desplaçar \(\overrightarrow{F}\) fins que sigui perpendicular a \(\overrightarrow{r}\), de forma que el \(sin(\varphi)\) valgui 1.
Paral·lelisme entre el moviment linial i angular#
Al igual que, segons la segona llei de Newton, una força genera una acceleració linial, un moment genera una acceleració angular.
\(\begin{array}{rcl} \overrightarrow{F}=m \cdot \overrightarrow{a} & \overrightarrow{\Gamma} = \textbf{I} \cdot \overrightarrow{\alpha} \end{array}\)
On \(\textbf{I}\) és el moment d’inèrcia, un concepte que utilitza eines matemàtiques avançades com són les integrals i les matrius, recursos que es desenvolupen a matemàtiques de 2n de batxillerat. Trobareu una explicació detallada al tema sólido rígido[FG16e]. El seu estudi utilitza càlculs del tipus
\(I = \sum m_i \cdot r_i^2\)
En realitat les coses són més complicades
\(\begin{array}{rcl} \overrightarrow{p} \equiv m \cdot \overrightarrow{v} & \overrightarrow{L} \equiv \overrightarrow{r} \times \overrightarrow{p} = \textbf{I} \cdot \overrightarrow{\omega} \\ \overrightarrow{F} = \frac{d \overrightarrow{p}}{dx} & \overrightarrow{\Gamma} = \frac{d \overrightarrow{L}}{dx} \end{array}\)
on \(\overrightarrow{L}\) és el moment angular
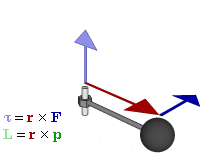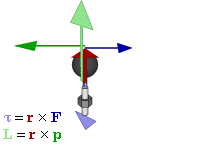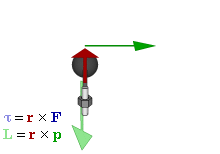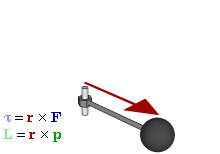
A partir d’aquí podem fer un paral·lelisme entre les equacions dels moviments linials i angulars:
Acceleració constant
\(\begin{array}{cc} \overrightarrow{v} = \overrightarrow{a} \cdot t & \overrightarrow{\omega} = \overrightarrow{\alpha} \cdot t \\ \overrightarrow{x} = \overrightarrow{x_0} + \overrightarrow{v} \cdot t + \frac{1}{2} \cdot \overrightarrow{a} \cdot t^2 & \overrightarrow{\varphi} = \overrightarrow{\varphi_0} + \overrightarrow{\omega} \cdot t + \frac{1}{2} \cdot \overrightarrow{\alpha} \cdot t^2 \end{array}\)
Potència i treball
\(\begin{array}{cc} P = \overrightarrow{F} \cdot \overrightarrow{v} & P = \overrightarrow{\Gamma} \cdot \overrightarrow{\omega} \\ W = \overrightarrow{F} \cdot \overrightarrow{x} & W = \overrightarrow{\Gamma} \cdot \overrightarrow{\varphi} \end{array}\)
Conservació del moment angular#
Si sobre el cos no actua cap moment el moment angular es conserva. Però podem tenir una acceleració angular per compensar canvis en el moment d’inèrcia. Aquesta relació és molt coneguda entre les patinadores i altres atletes, com podeu veure al vídeo
Show code cell source
from IPython.display import YouTubeVideo
YouTubeVideo('bSrAoFB3jBU')
Condicions d’equilibri#
Si volem que un objecte en repòs no es mogui, cal que no hagi cap tipus d’acceleració, es a dir, que la suma de forces sigui 0 i la suma de moments sigui 0:
\(\sum \overrightarrow{F_i} = \overrightarrow{0}\)
\(\sum \overrightarrow{\Gamma_i} = \overrightarrow{0}\)
Diagrama del cos lliure#
Per aplicar aquestes condicions d’equilibri és molt útil dibuixar el diagram del cos lliure, on només dibuixem el cos que estudiem i les forces i moments aplicats sobre ell.
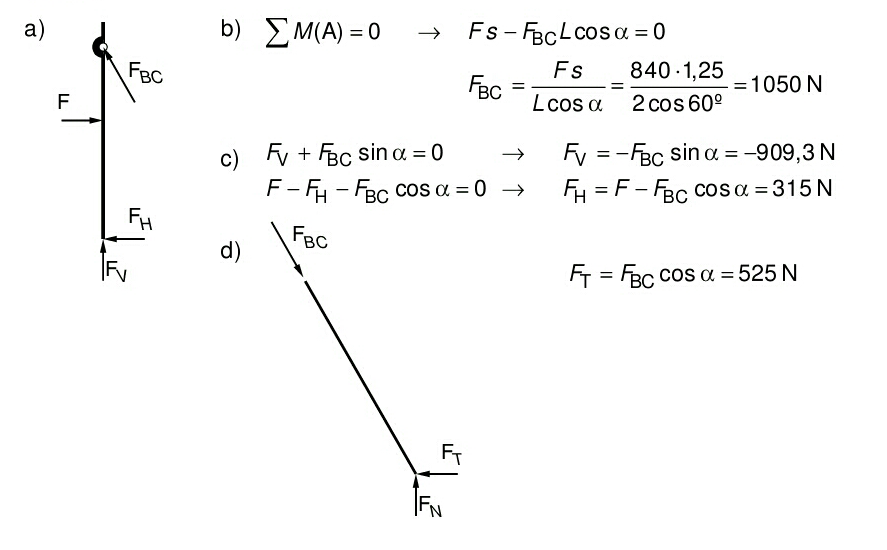
Exemple: PAU 2010 S1 3A
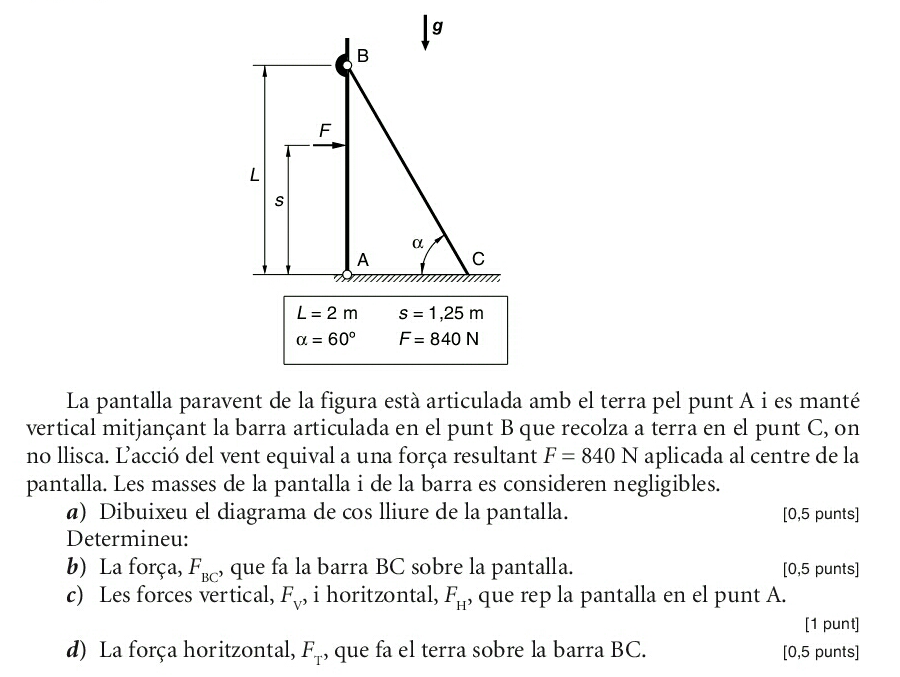
Solució