Pressupost del projecte#
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
En realitat cal parlar de dos pressupostos diferents: el presupost del prototip, que és el cost del disseny i construcció d’un prototip viable; i el pressupost del producte, que és el cost del producte quan es posa a la venda i es fabrica en grans quantitats.
Pressupost del prototip#
Tindrem dos tipus de despeses:
Recursos Materials: Investigar els costos dels materials necessaris per dur a terme el prototip.
Recursos Humans: Cal analitzar els costos associats amb el temps del personal, incloent-hi salaris, impostos i altres despeses relacionades.
Veiem un exemple (dades reals del TR de Blai Harder PROTOTIP D’UNA CASA INTEL·LIGENT CONTROLADA AMB UN COMANDAMENT PS3).
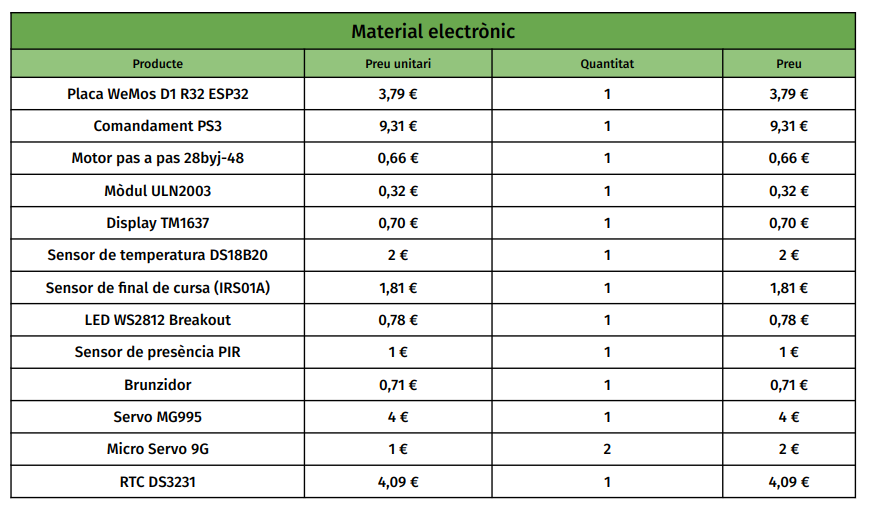
Calculem el cost de materials:
ME=3.79+9.31+0.66+0.32+0.70+2+1.81+0.78+1+0.71+4+2+4.09
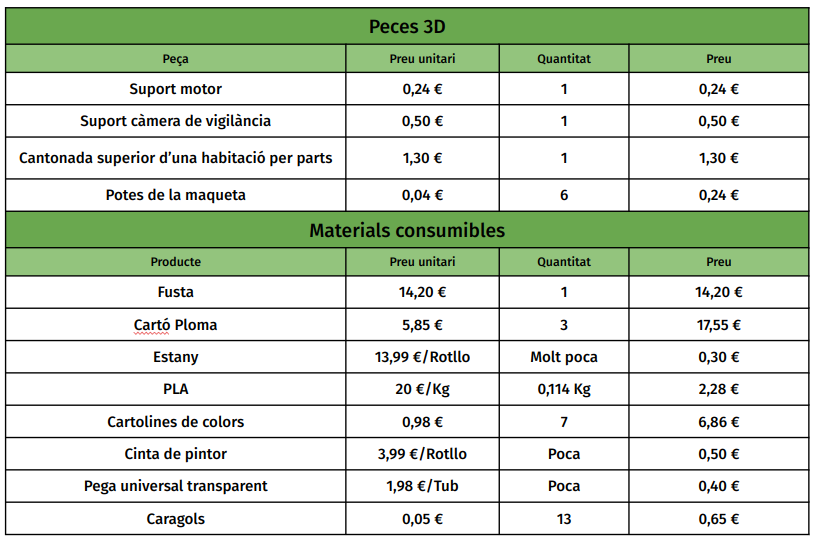
P3D=0.24+0.50+1.30+0.24
MC=14.20+17.55+0.30+2.28+6.86+0.50+0.40+0.65
CM=ME+P3D+MC
CM
76.19
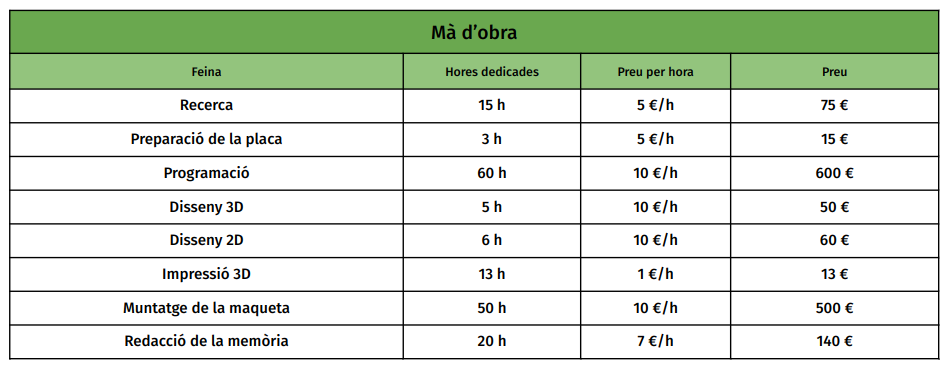
Ara el cost de la mà d’obra:
CH=75+15+600+50+60+13+500+140
CH
1453
En total aquest prototop té un cost de
CP=CM+CH
CP
1529.19
Pressupost del producte#
Si us fixeu, gran part del cost del prototip ha estat la programació i el muntatge de la maqueta. Són pràcticament el 80% del cost del prototip.
Però si comercialitzem aquest producte, no caldra tornar a fer la programació: el codi ja el tenim del prototip. Com amolt trigarem 5 minuts en carregar el mateix codi en el producte.
Per altra banda, el muntatge de la maqueta ha estat molt artesanal. Si en lloc de tallar manualment la fusta i el cartro ploma fem servir una talladora laser el preu cau ràpidament. De fet, en Blai té els fitxers DXF dels perfils a la seva memòria, en 15 minuts el tindria adaptats a la talladora laser.
De fet, de tots els apartats de mà d’obra únicament hauríem d’incloure al producte la placa, la càrrega del programa, la supervisió de la impressió 3D i el cost del nou muntatge optimitzat. D’aquesta manera podem reduir aquests 1453 € a, posem un marge generós, 200 €.
Es clar que si comercialitzem el producte podem carregar una petita part del cost del prototip sobre el producte, i així recuperar el cost de R+D+I.
Posem que fem 1000 unitats del producte. Com el prototip ha costat 1530 € carreguem 1,53 € del prototip en cada producte.
Així el cost final del producte seria, per a una producció de 1000 unitats:
CH2=200
PP=1.53
CP2=CM+CH2+PP
CP2
277.71999999999997
Si posem el producte a un preu de venda de 400 €, ens podem emportar uns bons beneficis.
Anàlisi de costos. Càlcul del punt mort#
En realitat les coses són una mica més complicades. I si ens equivoquem i no venem les 1000 unitats? A partir de quin volum de vendes tindríem beneficis?
Cal diferenciar 2 tipus de costos:
costos fixos: no varien amb la producció
costos variables varien proporcionalment amb la producció
En el nostre cas el cost del prototip és un cost fix. El tenim ecara que no es vengui res. El cost del material és un cost variable, així com el pru de la mà d’obra: si les ventes no van bé no comprem més materials ni montem més producte. Per altra banda produir 1000 unitats pot gastar molt la nostra impressora 3D. Afegim un nou cost fix, la compra d’una impressora 3D per 250 €.
Per tant ara tenim de cost fix:
CF=1529.19+250
CF
1779.19
El cost variable per unitat és
CV=CM+CH2
CV
276.19
Per tant per n unitats tenim unes despeses
\(d=CF+n\cdot CV\)
I si venen les n unitats al preu de 400€ = PV tindremu ns ingressos
\(i=n \cdot PV\)
Fem la gràfica d’aquestes 2 funcions:
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
PV = 400
n = np.linspace(0, 50, 50)
plt.plot(n, n*PV, label='$ingressos$')
plt.plot(n, CF+n*CV, label='despeses')
plt.xlabel('n')
plt.ylabel('€')
plt.title("Anàlisi de costos")
plt.legend();
plt.show();
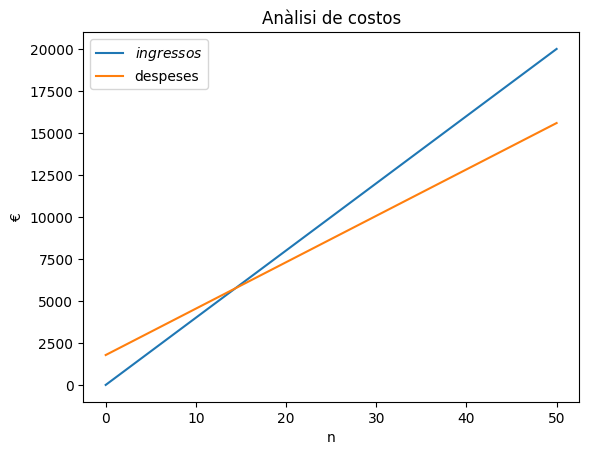
Fixeu-vos com es creuen les dues rectes al voltant de les 15 unitats. A la deta tindrem beneficis; a l’esquerra pèrdues.
El punt de tall se’n diu punt mort. Anem a calcular-lo exactament:
\(CF+n\cdot CV = n \cdot PV \Rightarrow n \cdot PV - n\cdot CV = CF \Rightarrow n \cdot (PV - CV) = CF\)
\(\Large \Rightarrow n = \frac{CF}{PV - CV} \)
n=CF/(PV-CV)
n
14.370325498748082
El que jo deia: hem de vendre 15 per no tenir pèrdues.