Corrent Altern

Corrent Altern#

Pàgina en desenvolupament

Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.

Típicament la generació d’energia elèctrica a les centrals es produeix en forma de corrent altern (AC). Aquet tipus de corrent té avantatges, com ara simplificar els generadors, alternadors en aquest cas; i reduir les pèrdues en la seva transmissió gràcies a la conversió a molt alt voltatge (MAT) als transformadors. En el tema Màquines elèctriques estudiarem aquests dispositius.

Resposta AC d’una resistència#

Veiem l’efecte d’un corrent AC sobre una resistència:

Com veiem, la resistència rep un corrent sinosoidal del generador de la forma:

\(u(t) = U_{max} \cdot sin(\omega t)\)

on

\(U_{max}\) és el valor màxim de la tensió
\(\omega\) és la pulsació, \(\omega = 2 \pi f\)

i per la resistència circula un corrent

\(i(t) = I_{max} \cdot sin(\omega t)\)

amb \(I_{max} = U_{max} / R\)

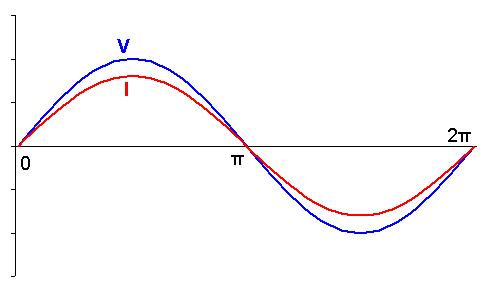
A Espanya es treballava a 50Hz i 220V, però al 2003 es va canviar a 230V per adaptar-nos a la normativa europea [Sol04].

230V? Segons la gràfica \(U_{max}=325 \ V\)

Valor eficaç de la tensió AC#

Quan es referim a una tensió AC no diem el valor màxim \(U_{max}\), diem el valor d’una tensió contínua DC que produeix el ateix efecte Joule sobre una resistència. Aquest valor rep el nom de valor eficaç o valor RMS. A la gràfica veieu que \(V{rms} = 230 V\)

Fixeu-vos en la gràfica de la potència. No és constant, és el producte de \(v(t) \ i(t) / R\) per a cada instant. Si volem el promig hem d’utilitzar integrals. Calculem el promig per a un periode (\(T = \frac{1}{f}\))

\(\Large P_{ef} = \frac{1}{T} \int_{0}^{T}u(t)\ i(t)) \ dt = \frac{1}{T} \int_{0}^{T}u(t)\ \frac{u(t))}{R} \ dt = \frac{1}{RT} \int_{0}^{T}{u(t)}^2 \ dt =\)

\(\Large= \frac{1}{RT} \int_{0}^{T}U_{max}^2 \ sin^2(t) \ dt = \frac{U_{max}^2}{RT} \int_{0}^{T} \ sin^2(t) \ dt = \frac{U_{max}^2}{RT} \left[ \frac{x}{2} - \frac{\sin(2x)}{4} \right]_0^T =\)

\(\Large= \frac{U_{max}^2}{RT}\frac{T}{2} = \frac{U_{max}^2}{2R} = \frac{U_{ef}^2}{R} \)

\(\Large \Rightarrow U_{ef} \equiv \frac{U_{max}}{\sqrt{2}}\)

En el nostre cas, amb els 230V actuals

from numpy import *
Uef=230
Umax=Uef*sqrt(2)
Umax

325.2691193458119

Abans del 2003, amb 220V:

from numpy import *
Uef=220
Umax=Uef*sqrt(2)
Umax

311.1269837220809

Així, una tensió Ac es pot caracteritzar per:

on

Valor de pic \(U_{max}\)
Valor pic a pic \(U_{pp} = 2 \ U_{max}\)
Valor eficaç \(\large U_{ef} = \frac{U_{max}}{\sqrt(2)}\)
Període \(T\)

Resposta AC d’una bobina#

Veiem ara com respon una bobina al corrent altern:

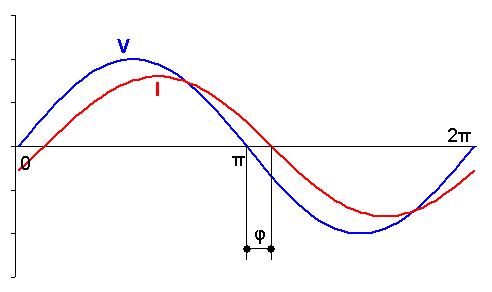
Que està passant? La tensió i la intensitat no estan sincronitzats. Hi ha un desfase, la intensitat va enderrerida a la tensió

Resposta AC d’un condensador#

Provem ara amb un condensador

Passa quelcom semblant. Ara la intensitat va avançada a la tensió:

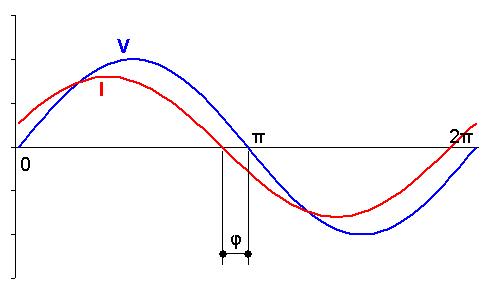
Quina màgia es aquesta? Necessitarem més eines per tractar aquest problema, que veurem als temes següents.