Lleis de Kirchoff#
Llei dels nusos#
Aquesta llei té en compte el principi de conservació de la càrrega. Per tant, si en un punt es connecten diferents conductors (punt anomenat nus), el balanç de les intensitats que arriben al punt (fletxa d’entrada, signe +) i que surten del punt (fletxa de sortida, signe -) és zero.
Matemàticament s’expressa:
\(\sum I_i = 0\)
Llei de les malles#
Aquesta llei té en compte el principi de conservació de l’energia. Si seguim el recorregut tancat (recorregut anomenat malla) realitzat per una càrrega les diferencies de potencials aportades pels generadors (forces electromotrius, \(\varepsilon_i\)) han de ser igual a les consumides per les resistències (caigudes ohmiques \(I_i \cdot R_i\)) i altres receptors (forces contraelectromotrius, \(\varepsilon'_i\)).
Cal tenir present el signe dels generadors: si ajuden a la nostra càrrega a realitzar el circuit (+) o el dificulten (-); així com la consistència del recorregut amb el sentit de les fletxes de les intensitats: (+) si anem amb el mateix sentit, (-) si anem en sentit contrari.
També és important no oblidar les resistències internes de generadors i receptors, si no són negligibles.
Matemàticament:
\(\sum \varepsilon_i - \sum \varepsilon'_i = \sum I_i \cdot R_i \)
Si el nostre circuit no té nusos, es a dir, té una única malla, tindrem una única intensitat que podrem aillar fàcilment de l’equació de la malla:
\(I = \frac{\sum \varepsilon_i - \sum \varepsilon'_i }{R}\)
Equació que és conneix com Llei d’Ohm generalitzada,
En el cas més habitual tenim m malles i n nusos. Haurem de ressoldre un sistema d’eqüacions amb m-1 equacions utilitzant la llei de les malles i n-1 eqüacions utilitzant la llei dels nusos.
Exemple de resolució#
1)#
Trobar \(I_{1}\), \(I_{2}\) i \(I_{3}\)
Dades: \(R_{1} = 2 \ \Omega\), \(R_{2} = 6 \ \Omega\), \(R_{3} = 4 \ \Omega\). \(\mathcal{E}_{1} = 5 \ V\), \(\mathcal{E}_{2} = 12 \ V\)
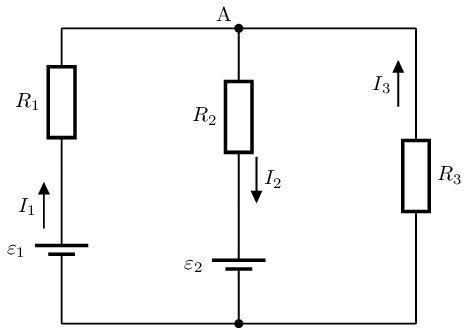
\(I_1+I_3-I_2=0\)
\(-\varepsilon_2+\varepsilon_1=I_2 \cdot R_2+I_1 \cdot R_1\)
\(\varepsilon_2=-I_3 \cdot R_3-I_2 \cdot R_2\)
\(I_1+I_3-I_2=0\)
\(-12 V+ 5 V=I_2 \cdot 6 \Omega +I_1 \cdot 2 \Omega\)
\(12 V=-I_3 \cdot 4 \Omega-I_2 \cdot 6 \Omega\)
S.I. :
\(I_1+I_3-I_2=0\)
\(-7=6 \cdot I_2 + 2 \cdot I_1\)
\(12=-4 \cdot I_3 - 6 \cdot I_2\)
from sympy import *
x, y, z = symbols("x y z")
solve([Eq(x+z-y, 0), Eq(6*y+2*x,-7 ), Eq(-4*z-6*y,12 )],[x,y,z])
{x: 1/22, y: -13/11, z: -27/22}
1/22, -13/11, -27/22
(0.045454545454545456, -1.1818181818181819, -1.2272727272727273)
\(I_1 = 45,45 A\)
\(I_2 = -1,182 A\)
\(I_3 = -1,227 A\)