Ctrl+K

Circuits AC

Circuits AC#

Estudi d’un circuit RC sèrie#

Tornem al nostre circuit d’exemple. Ara trobarem tots els resultats disponibles de forma sistemàtica.

Un circuit sèrie amb una resistència \(R = 10 \ \Omega\) i un condensador \(C = 162,48 \ \mu F\) està connectat a una xarxa monofàsica \(U = 200 V\) i \(f = 50 Hz\)

\[\begin{split} \begin{matrix} X_{C} = \frac{-j}{C \omega} & \omega = 2 \pi f & Z = R + X_{C} \\ \end{matrix} \end{split}\]
Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

Dades#

R = 10
C = 162.48 * 10**(-6)
U = 220
f = 50
w = 2 * np.pi * f

Càlcul de les impedàncies#

Xc = 0 -1j/(C*w)
Xc

-19.590711852769j

\(X_{C} = 19.59_{-90^{\circ}} \ \Omega\)

Z = R + Xc
Z

(10-19.590711852769j)

modZ = np.abs(Z)
modZ

21.995362940816044

angZ = np.degrees(np.angle(Z))
angZ

-62.958143957668284

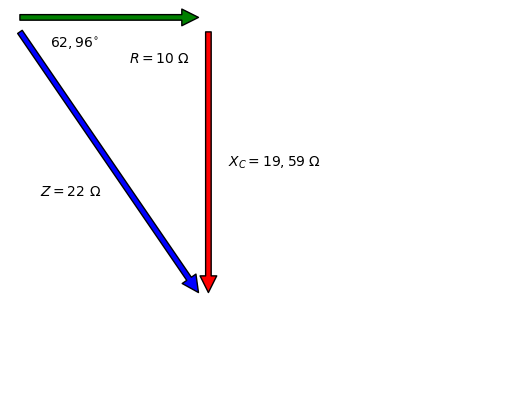
\(Z = 22_{-62,96^{\circ}} \ \Omega\)

Hide code cell source 
%matplotlib inline


plt.annotate('', xy=(np.real(Z), np.imag(Z)), xytext=(0, 0),
             arrowprops=dict(facecolor='blue', shrink=0.05),
             )

plt.annotate('', xy=(np.real(Z), 0), xytext=(0, 0),
             arrowprops=dict(facecolor='green', shrink=0.05),
             )

plt.annotate('', xy=(np.real(Z), np.imag(Z)), xytext=(np.real(Z), 0),
             arrowprops=dict(facecolor='red', shrink=0.05),
             )

plt.annotate("$Z = 22 \ \Omega$", xy=(1.5, -12))
plt.annotate("$R = 10 \ \Omega$", xy=(6, -3))
plt.annotate("$X_{C} = 19,59 \ \Omega$", xy=(11,-10))
plt.annotate("$62,96^{\circ}$", xy=(2,-2))

plt.xlim(0, 25)
plt.ylim(-25, 0)
plt.axis('off')
plt.show()
_images/fe2bb2bb1d60ebb4bdce1c5605b37c23dc8f8b08b4844c76c9d28ae24785a4da.png

Factor de potència#

fdp = np.cos(angZ)
fdp

0.9920358997298501

\(cos(\varphi) = 0,9920\)

Intensitat#

I = U/Z
I

(4.547371291596367+8.908624066121842j)

modI = np.abs(I)
modI

10.00210819853095

angI = np.degrees(np.angle(I))
angI

62.958143957668284

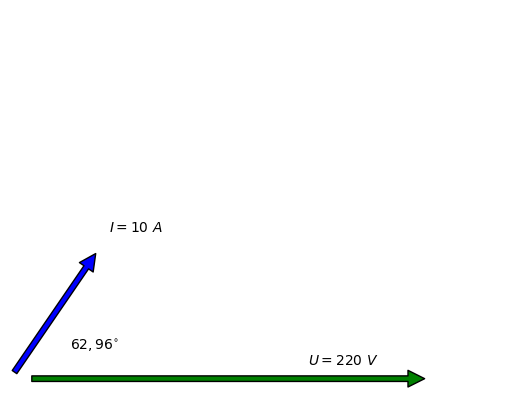
\(I = 10_{62,96^{\circ}} \ A\)

Hide code cell source 
%matplotlib inline


plt.annotate('', xy=(10*np.real(I), 10*np.imag(I)), xytext=(0, 0),
             arrowprops=dict(facecolor='blue', shrink=0.05),
             )

plt.annotate('', xy=(U, 0), xytext=(0, 0),
             arrowprops=dict(facecolor='green', shrink=0.05),
             )

plt.annotate("$I = 10 \ A$", xy=(50, 100))
plt.annotate("$U = 220 \  V$", xy=(150, 10))
plt.annotate("$62,96^{\circ}$", xy=(30,20))

plt.xlim(0, 250)
plt.ylim(0, 250)
plt.axis('off')
plt.show()
_images/9119f4df00ee75a60337a8c8e3c11ecc428acbd4f9ab19542715d2dc1a03737b.png

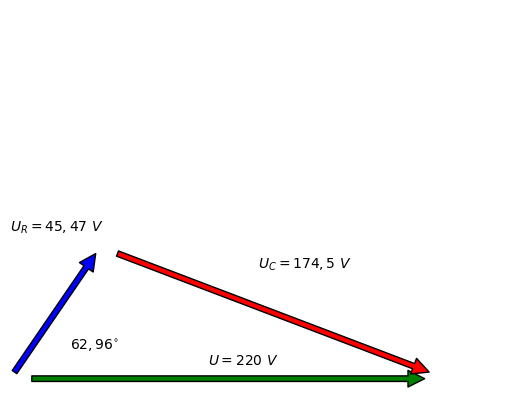
Tensions#

Ur = R * I
Ur

(45.47371291596367+89.08624066121843j)

modUr = np.abs(Ur)
modUr

100.02108198530951

angUr = np.degrees(np.angle(Ur))
angUr

62.958143957668284

\(U_{R} = 100_{62,96^{\circ}} \ V\)

Uc = Xc * I
Uc

(174.52628708403634-89.08624066121843j)

modUc = np.abs(Uc)
modUc

195.9484196376383

angUc = np.degrees(np.angle(Uc))
angUc

-27.04185604233172

\(U_{C} = 196_{-27,04^{\circ}} \ V\)

Hide code cell source 
%matplotlib inline


plt.annotate('', xy=(np.real(Ur), np.imag(Ur)), xytext=(0, 0),
             arrowprops=dict(facecolor='blue', shrink=0.05),
             )

plt.annotate('', xy=(U, 0), xytext=(0, 0),
             arrowprops=dict(facecolor='green', shrink=0.05),
             )

plt.annotate('', xy=(U, 0), xytext=(np.real(Ur), np.imag(Ur)),
             arrowprops=dict(facecolor='red', shrink=0.05),
             )


plt.annotate("$U_{R} = 45,47 \ V$", xy=(0, 100))
plt.annotate("$U_{C} = 174,5 \ V$", xy=(125, 75))
plt.annotate("$U = 220 \  V$", xy=(100, 10))
plt.annotate("$62,96^{\circ}$", xy=(30,20))

plt.xlim(0, 250)
plt.ylim(0, 250)
plt.axis('off')
plt.show()
_images/e5318cc05d25b3cb0aeeaceeaa81e58c22490b47d84327adaabad04ae3099fa5.png

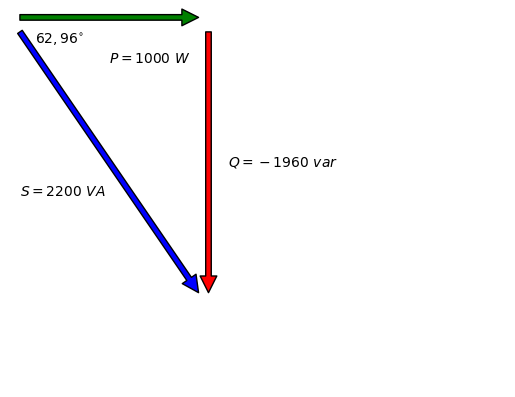
Potències#

S = U * np.conj(I)
S

(1000.4216841512007-1959.8972945468051j)

modS = np.abs(S)
modS

2200.463803676809

angS = np.degrees(np.angle(S))
angS

-62.958143957668284

\(S = 2200_{-62,96^{\circ}} \ VA\)

P = np.real(S)
P

1000.4216841512007

\(P = 1000 \ W\)

Q = np.imag(S)
Q

-1959.8972945468051

\(Q = -1960 \ var\)

Hide code cell source 
%matplotlib inline


plt.annotate('', xy=(np.real(S), np.imag(S)), xytext=(0, 0),
             arrowprops=dict(facecolor='blue', shrink=0.05),
             )

plt.annotate('', xy=(np.real(S), 0), xytext=(0, 0),
             arrowprops=dict(facecolor='green', shrink=0.05),
             )

plt.annotate('', xy=(np.real(S), np.imag(S)), xytext=(np.real(S), 0),
             arrowprops=dict(facecolor='red', shrink=0.05),
             )

plt.annotate("$S = 2200 \ VA$", xy=(50, -1200))
plt.annotate("$P = 1000 \ W$", xy=(500, -300))
plt.annotate("$Q = -1960 \ var$", xy=(1100,-1000))
plt.annotate("$62,96^{\circ}$", xy=(125,-175))

plt.xlim(0, 2500)
plt.ylim(-2500, 0)
plt.axis('off')
plt.show()
_images/525f5c60c9c36bb2604bf05e127681bf562a31433c6ebc82c38cd60fded8b4b4.png

Circuit RL sèrie#

Els circuits RL són semblants als RC, però amb un canvi de signe de la impedància i la potència reactiva, ja que \(X_L = jL\omega\)

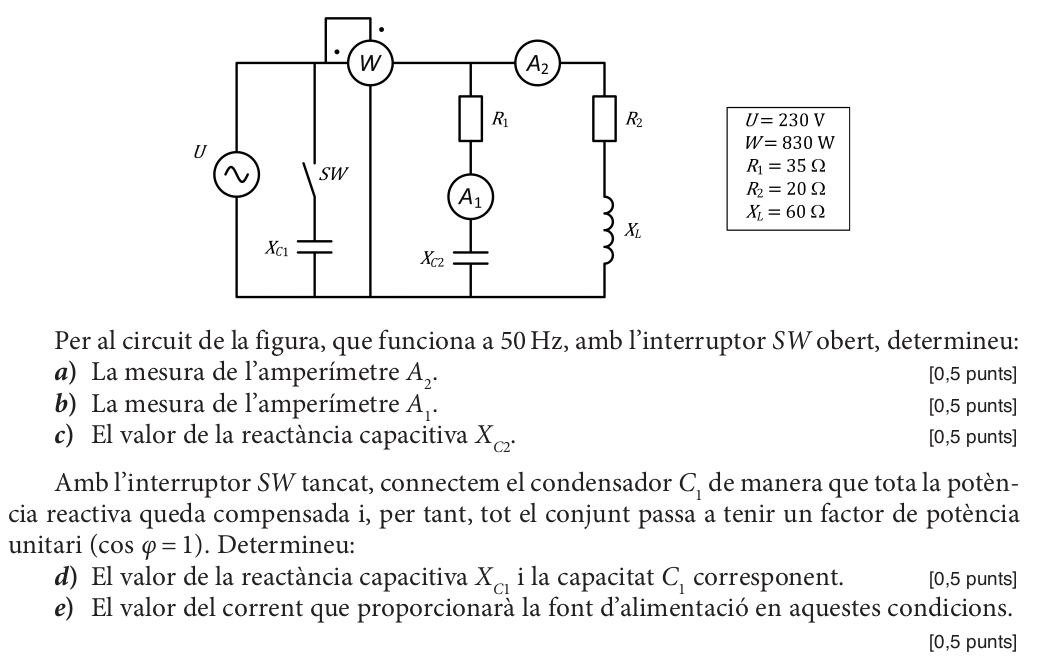
PAU ELECTROTÈCNIA 2015 S2 3A (1/2)#

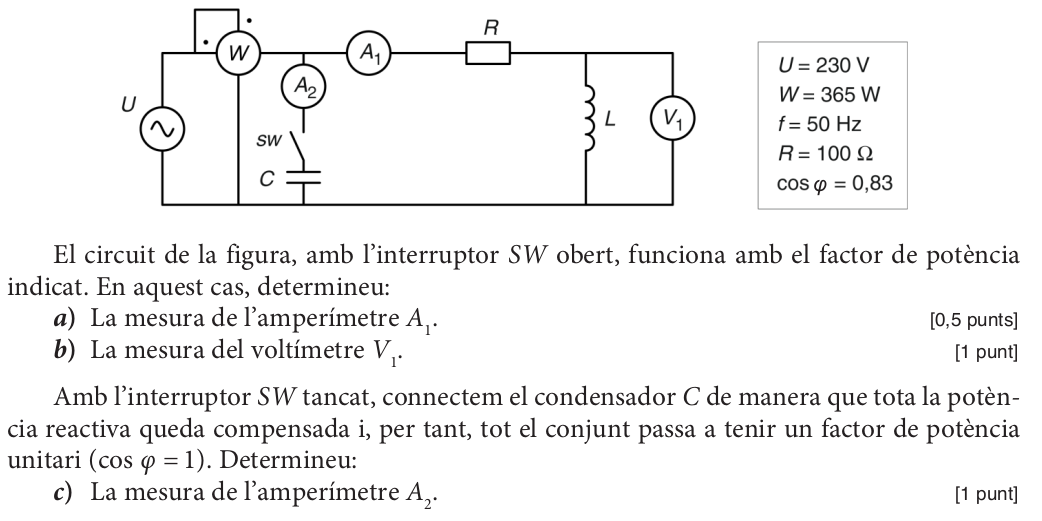
Anem a calcular els apartats a i b, que són d’un circuit RL sèrie. L’apartat c el comentarem més endavant.

a)

\(P={A_1}^2 \ R \Rightarrow A_1 =\Large \sqrt{\frac{P}{R}}\)

U=230
P=365
f=50
R=100
cosphi=0.83
from numpy import pi, sqrt 
w=2*pi*f
A1=sqrt(P/R)
A1

1.91049731745428

\(A_1=1,915 A\)

b)

\(P = S cos\varphi \Rightarrow S= \Large \frac{P}{cos\varphi}\)

\(Q=S sin\varphi = S \sqrt{1-sin^2\varphi}\)

S=P/cosphi
Q=S*sqrt(1-cosphi**2)
Q

245.28149108892936

\(Q = 245 \ var\), potència reactiva inductiva, hem agafat el signe + de l’arrel

\(Q=A_1V_1 \Rightarrow V_1=\Large \frac{Q}{A_1}\)

V1=Q/A1
V1

128.38620020454394

\(V_1 = 128,4 V\)

Circuit RLC sèrie#

En aquest cas el que hem de fer es primer sumar les impedàncies de l’eix imaginari \(X_C\) i \(X_L\). El resultat serà una impedància reactiva equivalent,capacitiva o inductiva, segons qui guanyi. Ara ja podem treballar el circuit com un RC o RL sèrie.

Ressonància#

Que pasa si \(X_L = X_C\)?

Apareix un fenòmen anomenat ressonància. La condició de ressonància és

\(X_L=X_C \Rightarrow L\omega=\Large \frac{1}{C\omega} \normalsize \Rightarrow \omega ^2 = \Large \frac{1}{LC} \normalsize \Rightarrow \omega_R= \Large \frac{1}{\sqrt{LC}}\)

Per a aquesta freqüencia el circuit es comporta com una resistència R, amb un factor de potència 1

Hide code cell source 
%%html
 <iframe src="https://www.falstad.com/circuit/circuitjs.html?ctz=CQAgjCAMB0l3BWcAWaAOZYDMYEE4xIAmBAdgDZyJk0QkFI6BTAWjDACgA3ENR9or0ZZB-EFnpQpMBNyEgiRZPLDJlYzLDx1pUaLJ59xWcvJKmNkxtf0cATvJEhkTp-0gcAxs9eCXggWlYeFxwUnQ8LDRSZDxIPDwiNBN1YM4AGxUwPydAsRYYYkhY+CICUkSsYgt7FTUfAPr3LwaUZX8FJSD4SFDs6EVyMoYEZHIsHAhC3o5Mo0V2pwWpKegxvFJsjaJ2NHZNqFr5hFMO8xWPbzOT1omLPR7QlgQBxKHkMnZKGNppjMcTLdAWIYIQiFhSBDyJtIWgqBtDgB7ZwgcjqZzxbTIGxTBQorAcZGkVHo7EJcDkGy0CCCYkE5GEElSMlYmyCdngYQcAAW4B0yA4QA" width="800" height="600"></iframe>

PAU ELECTROTÈCNIA 2017 S1 P3B#

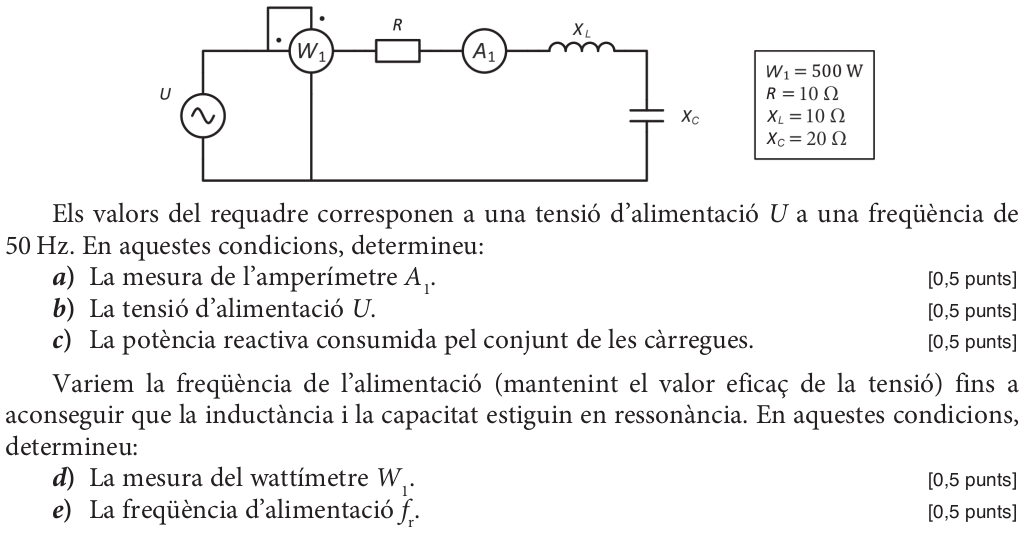
W1=500
R=10
XL=10
XC=20

a)

\(W_1=R {A_1}^2 \Rightarrow A_1=\Large \sqrt{\frac{W}{R}}\)

A1=sqrt(W1/R)
A1

7.0710678118654755

\(A_1=7,071 A\)

b)

\(U=ZI=\sqrt{R^2+(X_L-X_C)^2} \cdot A_1\)

Z=sqrt(R**2+(XL-XC)**2)
U=A1*Z
U

100.00000000000001

\(U=100,0 V\)

c)

\(Q=XI^2=(X_L-X_C){A_1}^2\)

Q=(XL-XC)*A1**2
Q

-500.00000000000006

\(Q = -500,0 var\)

d)

Ressonància \(\Rightarrow X_L=X_C\)

\(W_1=R{A_1}^2=R\Large (\frac{U}{Z})^2 = \frac{U^2}{R}\)

W1=U**2/R
W1

1000.0000000000003

\(W1 = 1000W\)

e)

\(X_C=\Large \frac{1}{C\omega} \normalsize \Rightarrow C=\Large \frac{1}{\omega X_C}\)

\(X_L = L\omega \Rightarrow L=\Large \frac{X_L}{\omega}\)

f=50
w=2*pi*f
C=1/(w*XC)
C

0.00015915494309189532

\(C=159,2 \mu F\)

L=XL/w
L

0.03183098861837907

\(L=31,83 mH\)

\(f_r=\Large \frac{1}{2\pi \sqrt {LC}}\)

fr=1/(2*pi*sqrt(L*C))
fr

70.71067811865476

\(fr=70,71 Hz\)

Ara que tenim el valor dels component podem simular el circuit i comprovar la ressonància:

Hide code cell source 
%%html
 <iframe src="https://www.falstad.com/circuit/circuitjs.html?ctz=CQAgjCAMB0l3BWcAWaAOZYDMYEE4xIAmBAdgDZyJMQkFJaBTAWjDACgA3ENBtongywC+tBkgaToCdgCdBIYSGRKlfSOwDGy1QJUD+UKLDi48A5gljJkRIllIIwJYslLHT7ADYLD+8M5GMJA4aFggzDBEbmFgyOTmRLhOEuwA9iAC5MhGmJDuRFJoRgICWOmZINm5kHjuhMbFEKWK7FjFDABiEOGFCqwgnbKMAI4ArowAdpoAnuxAA" width="800" height="600"></iframe>

Circuits AC paral·lel#

En aquest circuits és mé fàcil calcular i sumar vectorialment les intensitats de cada branca

També apareix el fenèmen de la ressonància, amb la mateixa condició:

\(\omega_R= \Large \frac{1}{\sqrt{LC}}\)

Hide code cell source 
%%html
 <iframe src="https://www.falstad.com/circuit/circuitjs.html?ctz=CQAgjCAMB0l3BWcAWaAOZYDMYEE4xIAmBAdgDZyIEsQkFI6BTAWjDACgA3Ec5EIskZ9w5RowiZYeOlDkwEHAMYhkyNKMZqNg8VFjwwyPCdNnzILNFzq8yUkUR40EGHE4B3XvzBjweIk0oDi8wAKCsRyDIEMso3y11aI4AGziJP0jGXTlXWGwXBARkMjRINEpIZHJggCd-QISGgSE5RzhYsMCcrJbxWN6c7T667xGukYkOnhEwIg0RJIlLRiQ9BWVVJO2kuY1xA3djcxPTAWhHUhMEMArIrAr+N0hPMd3wpc6PjV7Pr1+NMNPmkAelwPNciAWG4iL4wKQKERHIQcMgsKRRhN3o0Idl4F8cT94riBsTAbsSfVZhCJntctMxlgEIEREQHJCGLJ1tBFCphmzAsMmYEDvAXsdTidwNB0VdSHNynwcFg1Pp3LFWeyJgLgqFwjrBuyYv8ojr+UbUmCDVFhZDofk0WjSHAiOi0KQ0FgajF6tqteFbXiOnrArbeoHSYxbULmaMRLaJoHwB0APbJsZaSB4DFEHlqkhtdNYDhp4RPVRZnN557kAsQEWWEsCMtyITZ85rWAF7rNxsAC3Ask4QA" width="800" height="600"></iframe>

PAU ELECTROTÈCNIA 2015 S2 3A (2/2)#

Ara ja podem treballar l’apartat c que teníem pendent.

Com està en ressonància, \(Q_L + Q_C = 0 \Rightarrow A_2 = Q/U\)

Q=245.28
U=230
A2=Q/U
A2

1.0664347826086957

\(A2=1,066 A\)

PAU ELECTROTÈCNIA 2019 S4 P3A#

Contents