Assaig de tracció

A un assaig de tracció, una proveta normalitzada amb una secció \(s\) es somet a un força \(F\) de tracció. La tensió normal o esforç \(\sigma\) generat per la força \(F\) a la secció \(s\) té l’expressió:

\[\sigma = \frac{F}{s}\]

Quan l’esforç en la proveta està per sota del límit elàstic ens trobem a la zona elàstica on es cumpleix la llei de Hooke

\[\sigma = E\epsilon\]

on \(E\) és el mòdul de Young o Mòdul elàstic i \(\epsilon\) la deformació \(\epsilon = \frac{\Delta L}{L_{0}}\)

Si l’esforç supera el límit elàstic ens trobarem a la zona plàstica, on ja no es cumpleix la llei de Hooke i la deformació és permanent. Si continuem aplicant esforç a aquesta zona arribarem a un màxim, després d’ell ens costarà menys esforç deformar el material fins arribar a la tensió de ruptura on el material es trenca.

Aquestes assatjos es realitzen amb instruments com el de la fotografia, on s’utilitzen provetes normalitzades del material a estudiar.

Anem a estudiar un assaig amb un acer 4142 (trobareu diverses dades experimentals a ProfessorKazarinoff/staticsite i a https://pythonforundergradengineers.com/stress-strain-curve-with-python-and-matpotlib.html)

Show code cell source Hide code cell source

import numpy as np                        
import pandas as pd                       
import matplotlib.pyplot as plt           
import matplotlib.gridspec as gridspec    
import statistics as st                   
from scipy.stats import linregress        
from IPython.display import Markdown      


with open('data/Materials/acero_4142.npy', 'rb') as f:
    e = np.load(f)
    s = np.load(f)

e = e * 100    # treballarem amb la deformació en %

%matplotlib inline                               
plt.rcParams['figure.figsize'] = (16,7)           # determines the dimensions (size of the figure)
fig = plt.figure()
plt.plot(e, s)
plt.xlabel('$\epsilon$ [%]')
plt.ylabel('$\sigma$ [MPa]')
plt.title("Diagrama de tracció");

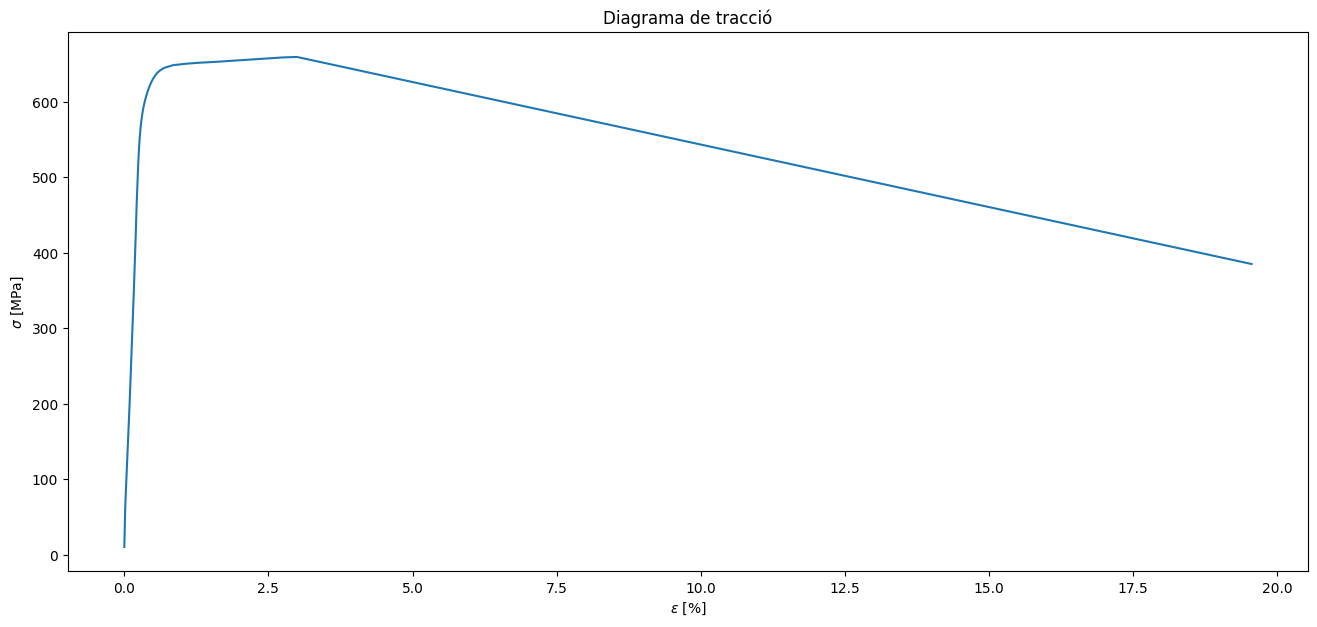
Si ens fixem en la zona elàstica, podrem fer una estimació del mòdul elàstic, agafant els punts que estan en línia recta

ms = linregress(e[35:102], s[35:102])
Es = ms[0]  
offset_acer = Es*(e - 0.2)
print("El Mòdul elàstic de l'acer 4142 és %d MPa" % Es )

El Mòdul elàstic de l'acer 4142 és 2022 MPa

Show code cell source Hide code cell source

%matplotlib inline                                       
plt.rcParams['figure.figsize'] = (9,7)     
plt.plot(e, s)
plt.plot(e, offset_acer,'k--')
plt.xlabel('$\epsilon$ [%]')
plt.ylabel('$\sigma$ [MPa]')
plt.title("Detall zona elàstica")
plt.axis([0,3,0,700])
plt.legend(["acer 4142 ($\sigma_{y}$)","0.2% off-set"],loc='lower right');

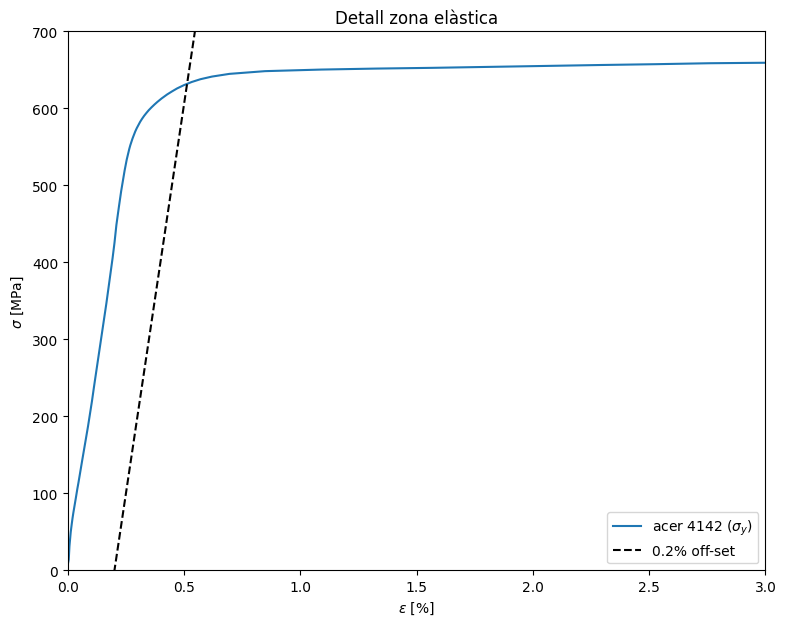
Podeu observar que hem dibuixat una líne paral·lela a la del comportament elàstic desplaçada un 0,2 % a la dreta. Com és molt difícil saber on acaba la recta i comenza la zona no linial, s’agafa com a valor experimental del límit elàstc el punt de tall de la corba amb aquesta recta desplaçada.

Show code cell source Hide code cell source

%matplotlib inline                             
plt.rcParams['figure.figsize'] = (9,7)     
plt.plot(e, s)
plt.plot(e, offset_acer,'k--')
plt.xlabel('$\epsilon$ [%]')
plt.ylabel('$\sigma$ [MPa]')
plt.title("Límit elàstic experimental")
plt.axis([0.45,0.55,620,640])
plt.legend(["acer 4142 ($\sigma_{y}$)","0.2% off-set"],loc='lower right');
#plt.savefig('acer_limit_elastic.png') 

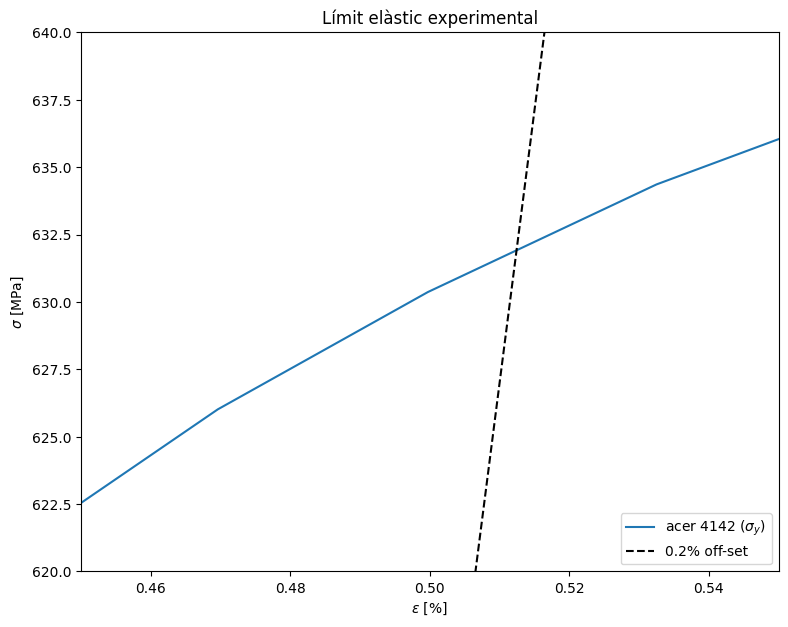
podem veure que el punt de tall es troba al voltant dels 630 MPa

Show code cell source Hide code cell source

#import plotly.offline as pyo
#pyo.init_notebook_mode(connected=True)

import plotly.express as px
import plotly.graph_objects as go
import plotly.io as pio


#pio.renderers.default = 'notebook'
#pio.renderers.default = 'jupyterlab'

#fig = px.scatter(x=e, y=s)
#fig = px.line(x=e, y=s, labels={'x':'$\epsilon [%]$', 'y':'$\sigma$$ [MPa]$'})
fig = go.Figure()
fig.add_trace(go.Scatter(x=e,y=s, mode='lines', name='real'))
fig.add_trace(go.Scatter(x=e,y=offset_acer, mode='lines', name='recta'))
fig.update_layout(
    xaxis_title=r'deformació [%]',
    yaxis_title=r'tensió [MPa]'
)
fig.update_xaxes(range=[0.51238, 0.51248])
fig.update_yaxes(range=[631.7, 632])
#fig.show("notebook") 
#fig.show("jupyterlab")
#fig.show(renderer="plotly_mimetype")
fig.write_html("assets/w3/diagtrac.html")

Amb aquest gràfic interactius podem precisar més fàcilment el punt de tall

Show code cell source Hide code cell source

%%html
 <iframe src="w3/diagtrac.html" width=600 height="500"></iframe> 

s_exp = 631.9
s_max = max(s)
print("L'acer 4142 té un límit elàstic de %.1f MPa i i una tensió màxima de %.1f MPa" %(s_exp, s_max))   

L'acer 4142 té un límit elàstic de 631.9 MPa i i una tensió màxima de 659.3 MPa

Una vegada que la proveta s’ha trencat a la tensió de ruptura, recupera la deormació elàstica. Per estimar la deformació plàstica que ens dona la ductibilitat del material caldrà restar la deformació elàstica amb una paral·lela a la recta elàstica. Podem fer una estimació amb aquest gràfic

Show code cell source Hide code cell source

%matplotlib inline
from ipywidgets import interactive
import matplotlib.pyplot as plt
import numpy as np

def f(b):
    offset_acer2 = Es*(e - b)    
    plt.figure()
    plt.plot(e, s)
    plt.plot(e, offset_acer2,'k--')
    plt.xlabel('$\epsilon$ [%]')
    plt.ylabel('$\sigma$ [MPa]')
    plt.title("Detall ruptura")
    plt.axis([19.2,19.6,0,450])
    plt.legend(["acer 4142 ($\sigma_{y}$)","0.2% off-set"],loc='lower right');    
    plt.show()

#interactive_plot = interactive(f, b=(19.2,19.6, 0.02))
#output = interactive_plot.children[-1]
#interactive_plot
f(19.36)

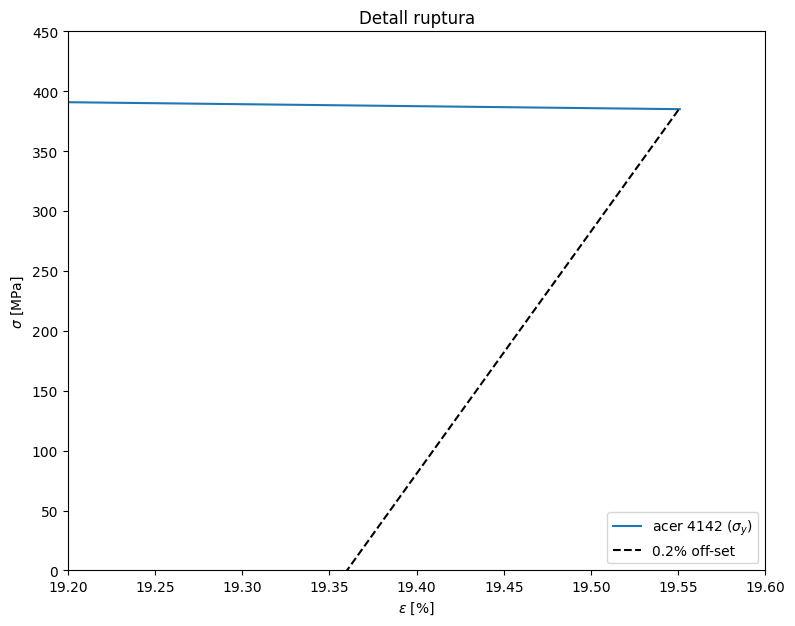
Podeu comprobar fàcilment que la deformació plàstica és d’un 19,36 %