Motor de corrent continu d’excitació independent#
L’esquema al rotor és molt semblant al motor d’imants permanents:

Però ara l’estator té una bobina amb resistència \(R_e\) alimentada amb una font externa \(U_e\) que genera el camp magnètic
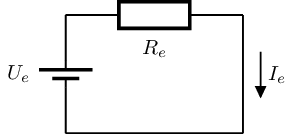
Condicions nominals#
No ha canviat res al rotor:
\(\Large I_i = \frac{U-\varepsilon}{r} \)
Al estator tenim ara un consum:
\(\Large I_e = \frac{U_e}{R_e} \)
Inversió de gir#
Cal invertir la polaritat de una de las fonts, però no de les dos a la vegada
Comportament a l’engegada#
Donada la similitud amb els motors d’imants permanents, hem de posar un reostat \(R_a\) amb sèrie amb el rotor per limitar la intensitat en l’engegada de forma que
\(I_a = \alpha \cdot I_n\)
\(1,5 \le \alpha \le 2,5\)
\(\Large \Gamma_a = \alpha \cdot \Gamma_n\)
Es a dir, si dupliquem la intensitat a l’engegada també dupliquem el parell
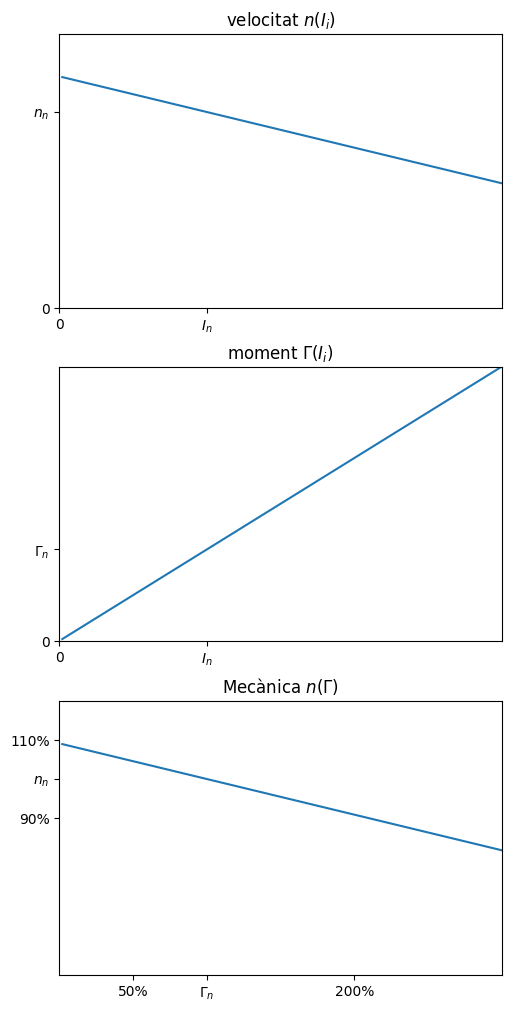
Corbes característiques#
Són molt semblants a les del motor d’imants permanents:
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
from math import pi
Pn=43E3
Un=420
In=121
nn=1133
UEn=200
IEn=6
En=Pn/In
r=(Un-En)/In
wn=nn*2*pi/60
kphin=En/wn
etan=Pn/(In*Un+IEn*UEn)
gn=kphin*In
x = np.linspace(0.02, 3, 300)
I = x*In
g = kphin*I
e = Un-I*r
w = e/kphin
eta=e*I/(Un*I+UEn*IEn)
fig, axs = plt.subplots(3, 1, figsize=(5, 10), layout='constrained')
axs[0].plot(I/In, w/wn)
axs[0].axis([0, 3, 0, 1.4])
axs[0].set_xticks([0,1], ['0','$I_n$'])
axs[0].set_yticks([0,1], ['0','$n_n$'])
axs[0].set_title('velocitat $n(I_i)$')
axs[1].plot(I/In, g/gn)
axs[1].axis([0, 3, 0, 3])
axs[1].set_xticks([0,1], ['0','$I_n$'])
axs[1].set_yticks([0,1], ['0','$\Gamma_n$'])
axs[1].set_title('moment $\Gamma(I_i)$')
axs[2].plot(g/gn, w/wn)
axs[2].axis([0, 3, 0, 1.4])
axs[2].set_yticks([0.8,1,1.2], ['90%','$n_n$','110%'])
axs[2].set_xticks([0.5,1,2], ['50%','$\Gamma_n$','200%'])
axs[2].set_title('Mecànica $n(\Gamma)$')
plt.show()
Aplicacions#
Com veiem aquest motor té un bon comportment: la variació de la càrrega només modifica lleugerament la velocitat, desenvolupant un parell proporcional al corrent. L’utilització dels elecroimants a l’estator permet fer motors potents i robusts.
Són motors ideals per màquines de velocitat pràcticament constant independentment de la càrrega: torns, trepants, ventiladors, bombes.
Especialment útils en màquines d’elevació on la càrrrega pot ser bruscament suprimida i un motor d’excitació sèrie podria embalar-se.
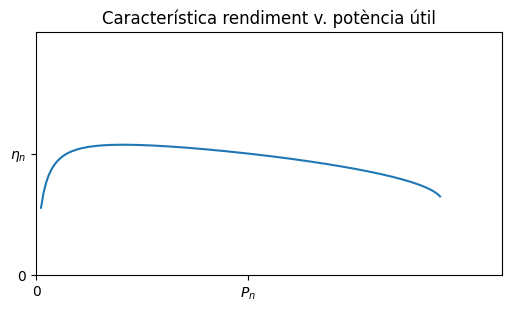
Rendiment#
Aquest motor té un rendiment nominal:
Show code cell source
p=I*e
fig, ax = plt.subplots(1, 1, figsize=(5, 3), layout='constrained')
ax.plot(p/Pn, eta/etan)
ax.axis([0, 2.2, 0, 2])
ax.set_xticks([0,1], ['0','$P_n$'])
ax.set_yticks([0,1], ['0','$\eta_n$'])
ax.set_title('Característica rendiment v. potència útil')
plt.show()
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
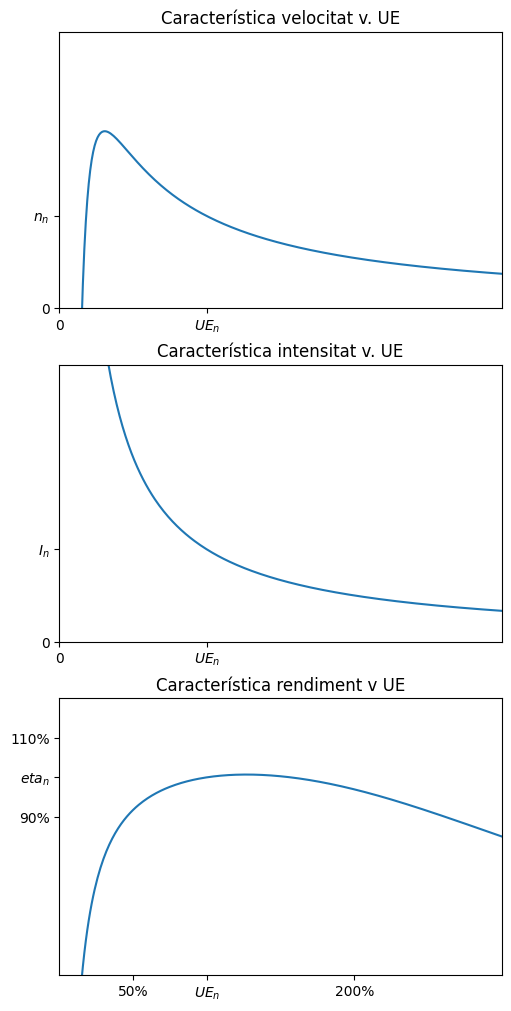
Variació de la tensió d’excitació externa#
Si canviem la tensió d’excitació externa en un factor \(\beta\) respecte el seu valor nominal \(U_e\):
\(U_{exc} = \beta \cdot U_e\)
també canviara el consum al estator:
\(\Large I_{exc} = \frac{\beta \cdot U_e}{R_e} = \beta \cdot I_e\)
Com aquesta intensitat genera el camp magnètic a l’estator, el flux variarà:
\(\Phi = \beta \cdot \Phi_n\)
Per tant la velocitat i el moment es veuran afectats:
\( \varepsilon = k \cdot \Phi \cdot \omega = k \cdot \beta \cdot \Phi_n \cdot \omega\)
\( \Gamma = k \cdot \Phi \cdot I_i = k \cdot \beta \cdot \Phi_n \cdot I_i\)
Es razonamble pensar que el momento es el nominal?
UE = x*UEn
IE = x*IEn
kphi = x*kphin
#sup g = gn
I = gn/kphi
e = Un-I*r
w = e/kphi
eta=e*I/(Un*I+UE*IE)
fig, axs = plt.subplots(3, 1, figsize=(5, 10), layout='constrained')
axs[0].plot(UE/UEn, w/wn)
axs[0].axis([0, 3, 0, 3])
axs[0].set_xticks([0,1], ['0','$UE_n$'])
axs[0].set_yticks([0,1], ['0','$n_n$'])
axs[0].set_title('Característica velocitat v. UE')
axs[1].plot(UE/UEn, I/In)
axs[1].axis([0, 3, 0, 3])
axs[1].set_xticks([0,1], ['0','$UE_n$'])
axs[1].set_yticks([0,1], ['0','$I_n$'])
axs[1].set_title('Característica intensitat v. UE')
axs[2].plot(UE/UEn, eta/etan)
axs[2].axis([0, 3, 0, 1.4])
axs[2].set_yticks([0.8,1,1.2], ['90%','$eta_n$','110%'])
axs[2].set_xticks([0.5,1,2], ['50%','$UE_n$','200%'])
axs[2].set_title('Característica rendiment v UE')
plt.show()
Exemple#
PAU ELECTROTÈCNIA 2020 S4 P4

PN=4E3
UN=280
IN=17.1
nN=1200
UEXCN=210
REXC=62
wN=nN*2*pi/60
a)
MN=PN/wN
MN
31.830988618379067
b)
EN=PN/IN
Ri=(UN-EN)/IN
Ri
2.6948462774870916
c)
U1=UN/2
M1=MN/2
I1=IN/2
E1=U1-Ri*I1
w1=E1/EN*wN
eta1=(M1*w1)/(U1*I1+UEXCN**2/REXC)*100
eta1
52.40292780228882
d)
UEXC2=UEXCN/2
M2=MN/4
I2=IN/2
n2=2636
w2=n2*2*pi/60
eta2=(M2*w2)/(UN*I2+UEXC2**2/REXC)
eta2
0.8541283847486928