Propietats elèctriques#
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
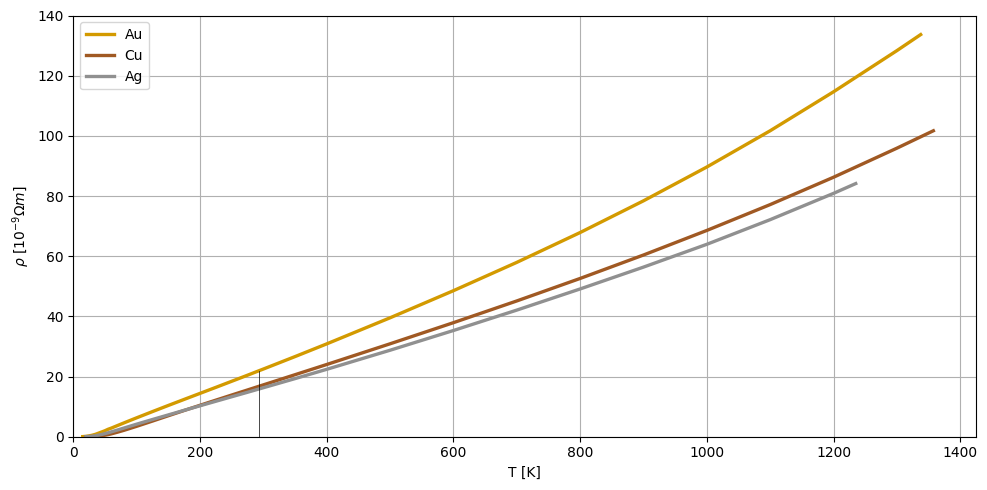
Resistivitat#
La resistència d’un conductor depèn de la longitud \(l\) d’aquest, de la seva secció \(s\) i del material:
\(R=\Large \rho \ \frac{l}{s}\)
on \(\rho\) és la resistivitat del material. Aquesta resistivitat no és constant: depèn de la temperatura:
\(\rho = \rho(T) = \rho_0 + c_1 \ \Delta T + ... \simeq \rho_0 \ (1+\alpha \ \Delta T) \)
Per exemple, per al coure \(ρ(20 °C) = 1,72·10⁻⁸ Ω·m\) i \(α = 0,0039 K⁻¹\)
Show code cell source
#Plot of the electrical resistivity of gold, copper and silver.
#Data is from (1979). "Electrical resistivity of copper, gold, palladium, and silver".
#Journal of Physical and Chemical Reference Data 8 (4): 1147–1298. DOI:10.1063/1.555614. ISSN 0047-2689
#Codi modificat de https://commons.wikimedia.org/w/index.php?curid=74783698
import matplotlib.pyplot as plt
import numpy as np
from math import *
# data: https://doi.org/10.1063/1.555614 TABLE 2.
# T in K, rho in 1e-8 Ohm*m
T_rho_Cu = np.array([
[20, 0.000798], [25, 0.00249], [30,0.00628], [35, 0.0127], [40, 0.0219],
[45, 0.0338], [50, 0.0498], [55, 0.0707], [60, 0.0951], [70, 0.152],
[80, 0.213], [90, 0.279], [100, 0.346], [125, 0.520], [150, 0.697],
[175, 0.872], [200, 1.044], [225, 1.215], [250, 1.385], [273.15, 1.541],
[293, 1.676], [300, 1.723], [350, 2.061], [400, 2.400], [500, 3.088],
[600, 3.790], [700, 4.512], [800, 5.260], [900, 6.039], [1000, 6.856],
[1100, 7.715], [1200, 8.624], [1300, 9.590], [1357.6, 10.169]
])
# data: https://doi.org/10.1063/1.555614 TABLE 5.
# T in K, rho in 1e-8 Ohm*m
T_rho_Au = np.array([
[15, 0.00376], [20, 0.0126], [25, 0.0282], [30, 0.0505], [35, 0.0798],
[40, 0.119], [45, 0.159], [50, 0.199], [55, 0.248], [60, 0.286], [70, 0.373],
[80, 0.459], [90, 0.544], [100, 0.628], [125, 0.835], [150, 1.039],
[175, 1.240], [200, 1.440], [225, 1.640], [250, 1.842], [273.15, 2.029],
[293, 2.192], [300, 2.249], [350, 2.663], [400, 3.085], [500, 3.952],
[600, 4.853], [700, 5.794], [800, 6.786], [900, 7.840], [1000, 8.964],
[1100, 10.169], [1200, 11.464], [1300, 12.832], [1337.58, 13.366]
])
# data: https://doi.org/10.1063/1.555614 TABLE 11.
# T in K, rho in 1e-8 Ohm*m
T_rho_Ag = np.array([
[20, 0.00322], [25, 0.00855], [30, 0.0184], [35, 0.0331], [40, 0.0529],
[45, 0.0763], [50, 0.103], [55, 0.131], [60, 0.161], [70, 0.224], [80, 0.288],
[90, 0.353], [100, 0.417], [125, 0.572], [150, 0.725], [175, 0.877],
[200, 1.028], [225, 1.178], [250, 1.328], [273.15, 1.466], [293, 1.586],
[300, 1.628], [350, 1.931], [400, 2.240], [500, 2.874], [600, 3.530],
[700, 4.208], [800, 4.911], [900, 5.637], [1000, 6.395], [1100, 7.214],
[1200, 8.088], [1235.08, 8.414]
])
plt.rcParams['figure.figsize'] = (10,5) # determines the dimensions (size of the figure)
fig = plt.figure()
plt.plot(T_rho_Au[:,0], 10.*T_rho_Au[:,1], '-', color='#d39a00', lw=2.4, label='Au')
plt.plot(T_rho_Cu[:,0], 10.*T_rho_Cu[:,1], '-', color='#a05923', lw=2.4, label='Cu')
plt.plot(T_rho_Ag[:,0], 10.*T_rho_Ag[:,1], '-', color='#909090', lw=2.4, label='Ag')
plt.grid(True)
plt.xlim(0)
plt.ylim(0, 140)
plt.xlabel('T [K]')
plt.ylabel(r'$\rho$ [$10^{-9}\Omega m$]')
plt.legend(loc='upper left')
plt.plot([293, 293], [0, 2.192e1], color='k', lw=0.5)
plt.tight_layout()
plt.show()
Superconductivitat#
Aquest fenomen quàntic apareix per a certs materials quan els refredem per sota d’una temperatura crítica \(T_c\). Es produeix una transició de fase i la resistivitat senzillament desapareix.
No es fàcil explicar l’aparició d’aquest fenomen. Diverses teories expliquen alguns dels tipus de superconductivitat observats, com la teoria BCS, però l’aparició de superconductors d’alta temperatura al 1987 (temperatures que es poden aconseguir amb nitrogen líquid, anteriorment els materials trobats tenien temperatures per sota de 40 K) encara no tenen explicació.
La recerca en aquest materials és clau: sense resistivitat es poden aconseguir electroimants potents, amb aplicació a la medicina, transport, reactors de fusió nuclear…
Piezoelectricitat#
Aquest efecte apareix en alguns materials que, en exercir pressió sobre ell, generen una diferència de potencial. Aquesta pot ser petita, com succeeix als micròfons dels mòbils i ordinador, o molt gran, com les tensions responsables de les guspires als encenedors piezoelèctrics.
També podem trobar l’efecte invers: aplicant una tensió sobre el material aquest es deforma. És el cas dels brunzidors piezoelèctrics i d’alguns actuadors, com els utilitzats als microscopis d’efecte tunel.
Show code cell source
from IPython.display import YouTubeVideo
YouTubeVideo('fHp95e-CwWQ')
Show code cell source
from IPython.display import YouTubeVideo
YouTubeVideo('VbTUsluY2xU')
Piroelectricitat#
Quan cares oposades d’alguns cristalls asimètrics s’exposen a la calor en forma de radiació infraroja, generen una petita càrrega elèctrica que es mesurable.
D’aquesta forma podem mesurar la temperatura d’un cos per la radiació infraroja que emet, sense contacte, a distància. Especialment útil per mesurar temperatures de forns o de persones en temps de pandèmia o per detectar la presència de persones en sistemes d’alarmes o automatització de llums de passadissos i serveis (sensors PIR).

Show code cell source
from IPython.display import YouTubeVideo
YouTubeVideo('qwaTJoY78OE')
Efecte Seebeck#
Aquest fenomen consisteix en la generació d’una diferència de potencial per efecte d’un gradient tèrmic. Aquest efecte es pot utilitzar per mesurar temperatures o per produir electricitat.
Un termoparell està constituït per dos fils de metalls diferents (A, B) soldats entre sí. Cada unió es col·loca a temperatura diferent (\(T_1\), $T_2) i es mesura la diferència de potencial generada, que es proporcional a la diferència de les dues temperatures:
\(U=(S_A-S_B) \ \Delta T\)
Tipus |
Materials |
\(S_A-S_B\) (μV/°C) |
|---|---|---|
J |
Fe-Constantà |
50 |
K |
Cromel-Alumel |
41 |
N |
Nicrosil-Nisil |
39 |
E |
Cromel-Constantà |
68 |
Efecte Peltier#
És l’efecte contrari al Seebeck: un corrent elèctric genera un flux de calor entre els termoparells, actuant com a bomba de calor:
\(\dot{Q}=p \ I\)
Si bé podríem fer servir els mateixos aliatges que hem vist a l’efecte Seebeck, s’han aconseguit elements Peltier molt eficients i econòmics utilitzant semiconductors de bismut telurat. Com el dopatge d’aquests semiconductors és fa malbé a la temperatura de fusió del Sn60Pb40 s’utilitza indi per soldar els elements, que té una temperatura de fusió més baixa.
Aquests mòduls Peltier també són molt eficients amb l’efecte Seebeck, per la qual cosa també s’utilitzen com a termopiles.

Potencial de contacte#
Quan dos metalls diferents es posen en contacte elèctric els electrons fluiran des del metall amb un nivell Fermi més alt fins al metall amb el nivell Fermi inferior, fins igualar els nivells. El fet que els nivells de Fermi siguin iguals, no vol dir que els potencials elèctrics siguin iguals. El potencial elèctric de cada material està controlat per la seva funció de treball Φ, de manera que els metalls diferents poden mostrar una diferència de potencial elèctric fins i tot en equilibri termodinàmic.
Metall |
Φ (eV) |
|---|---|
Ag |
4,7 |
K |
2,1 |
Au |
4,8 |
Mn |
3,8 |
Ca |
3,2 |
Na |
2,3 |
Cu |
4,1 |
Ni |
5,2 |
Aquest és el principi de funcionament de les piles. I per aquest motiu hem de vigilar quan posem en contacte dos metalls diferents, ja que poden generar problemes com la corrosió: monedes, pírcings, unions cargolades …