Primer principi. Transformacions termodinàmiques.#
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
Qüestions prèvies#
Un sistema està en equilibri termodinàmic quan les variables macroscòpiques \(p\), \(V\) i \(T\) no canvien.
La relació matemàtica entre les variables \(p\), \(V\) i \(T\) s’anomena eqüació d’estat. La més senzilla és la d’un gas ideal, i es la que farem servir aquest curs: \(pV = nRT\), on \(n\) és el nombre de mols, \(R\) la constant dels gasos, \(R = 8,3143 J/(K·mol)\).
La suma de energies de totes les partícules d’un sistema s’anomena energia interna \(U\). Al gasos ideals només depèn de la temperatura \(U = U(T)\).
El treball realitzat quan el sistema pasa de l’estat A amb volum \(V_A\) a l’estat B amb volum \(V_B\) val \(W= \int_{V_A}^{V_B}pdV\)
Quan una substància incrementa su temperatura de \(T_A\) a \(T_B\) la calor absorbida \(Q \ \) val \( \ Q = nc_V(T_B-T_A)\), on \(c_e\) és la calor específica a volum constant de la substància.
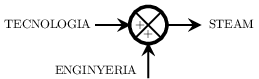
L”estat del sistema es pot representar amb un punt al diagrama p-V.
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
V=np.linspace(0.75, 1.25, 50)
p=1/V
p1=1
V1=1
fig, ax = plt.subplots(1, 1, figsize=(5, 3), layout='constrained')
plt.plot(V, p)
ax.scatter(V1, p1, s=50, facecolor='red', edgecolor='red')
plt.axhline(y=1, xmin=0, xmax=0.5, color='red',linestyle='--')
plt.axvline(x=1, ymin=0, ymax=0.5, color='red',linestyle='--')
ax.axis([0, 2, 0, 2])
ax.set_xticks([0,1], ['0','$V_A$'])
ax.set_yticks([0,1], ['0','$p_A$'])
ax.set_title('Diagrama p-V')
plt.xlabel('$V$', loc='right')
plt.ylabel('$p$', loc='top', rotation='horizontal')
plt.show()
Primer principi#
Si apliquem la llei de la conservació de l’energia a un sistema que rep una calor \(Q\) , realitza un treball \(W\) i experimenta una variació d’energia interna \(\Delta U\) obtenim:
\(Q = W + \Delta U\)
Transformacions termodinàmiques#
Quan un sistema varia alguna de les variables macroscòpiques les altres dues es veuen afectades donada la relació entre elles de l’eqüació d’estat.
Ens interessa calcular \(Q\), \(W\) i \(\Delta U\) en aquestes transformacions. No sempre e fàcil, però algunes transformacions es poden calcular de forma relativament fàcil, per la qual cosa s’utilitzen molt per modelitzar sistemes reals. La idea és aproximar fragments de les trajectòries reals a les màquines tèrmiques utilitzant aquests 4 processos.
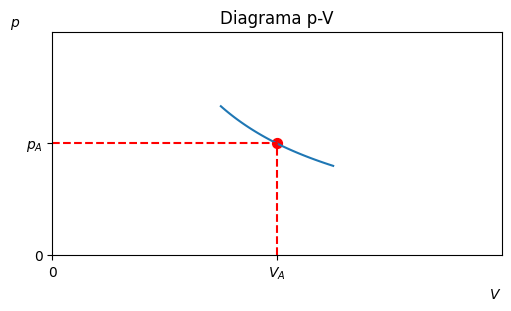
Procès isocòric#
Transformació a volum constant, \(\Delta V = 0\).
\(W = 0\)
\(Q =nc_V(T_B-T_A)\), on \(c_V\) és la calor específica a volum constant.
Per a gasos monoatòmics \(C_V = \frac{3}{2}R\)
Per a gasos diatòmics \(C_V = \frac{5}{2}R\)
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
p=np.linspace(0.5, 1.5, 50)
V=p/p
fig, ax = plt.subplots(1, 1, figsize=(5, 3), layout='constrained')
plt.plot(V, p)
plt.axhline(y=0.5, xmin=0, xmax=0.5, color='red',linestyle='--')
plt.axhline(y=1.5, xmin=0, xmax=0.5, color='red',linestyle='--')
plt.axvline(x=1, ymin=0, ymax=0.25, color='red',linestyle='--')
ax.axis([0, 2, 0, 2])
ax.set_xticks([0,1], ['0','$V_A=V_B$'])
ax.set_yticks([0,0.5,1.5], ['0','$p_A$','$p_B$'])
ax.set_title('Diagrama p-V procès isocòric')
plt.xlabel('$V$', loc='right')
plt.ylabel('$p$', loc='top', rotation='horizontal')
plt.show()
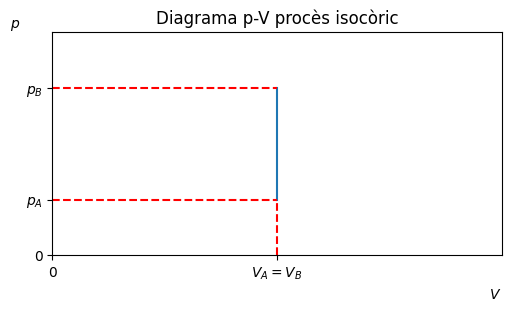
Procès isobàric#
Transformació a pressió constant, \(p_A = p_B \equiv p\).
\(W = p(B_B-V_A)\)
\(Q =nc_P(T_B-T_A)\), on \(c_P\) és la calor específica a pressió constant.
Per a gasos monoatòmics \(C_P = \frac{5}{2}R\)
Per a gasos diatòmics \(C_P = \frac{7}{2}R\)
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
V=np.linspace(0.5, 1.5, 50)
p=V/V
fig, ax = plt.subplots(1, 1, figsize=(5, 3), layout='constrained')
plt.plot(V, p)
plt.axhline(y=1, xmin=0, xmax=0.25, color='red',linestyle='--')
plt.axvline(x=0.5, ymin=0, ymax=0.5, color='red',linestyle='--')
plt.axvline(x=1.5, ymin=0, ymax=0.5, color='red',linestyle='--')
ax.axis([0, 2, 0, 2])
ax.set_xticks([0,0.5,1.5], ['0','$V_A$','$V_B$'])
ax.set_yticks([0,1], ['0','$p_A=p_B$'])
ax.set_title('Diagrama p-V procès isobàric')
plt.xlabel('$V$', loc='right')
plt.ylabel('$p$', loc='top', rotation='horizontal')
plt.show()
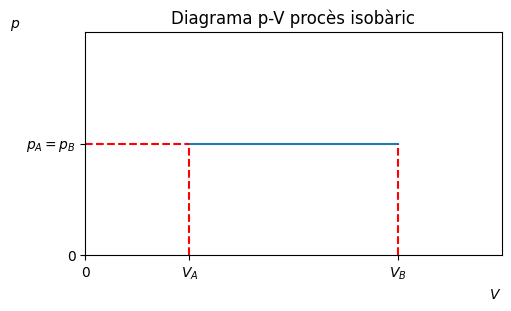
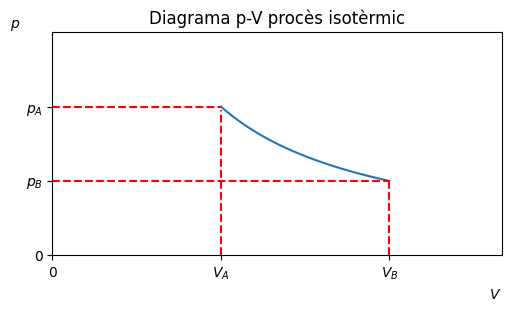
Procès isotèrmic#
Transformació a temperatura constant, \(\Delta T = 0\).
\(W = nRTln{\frac{V_B}{V_A}}\)
\(\Delta U = 0\)
\(Q = W\)
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
V=np.linspace(0.75, 1.5, 50)
p=1/V
fig, ax = plt.subplots(1, 1, figsize=(5, 3), layout='constrained')
plt.plot(V, p)
plt.axhline(y=1/0.75, xmin=0, xmax=0.375, color='red',linestyle='--')
plt.axhline(y=1/1.5, xmin=0, xmax=0.75, color='red',linestyle='--')
plt.axvline(x=0.75, ymin=0, ymax=0.65, color='red',linestyle='--')
plt.axvline(x=1.5, ymin=0, ymax=0.33, color='red',linestyle='--')
ax.axis([0, 2, 0, 2])
ax.set_xticks([0,0.75,1.5], ['0','$V_A$','$V_B$'])
ax.set_yticks([0,1.33,0.67], ['0','$p_A$','$p_B$'])
ax.set_title('Diagrama p-V procès isotèrmic')
plt.xlabel('$V$', loc='right')
plt.ylabel('$p$', loc='top', rotation='horizontal')
plt.show()
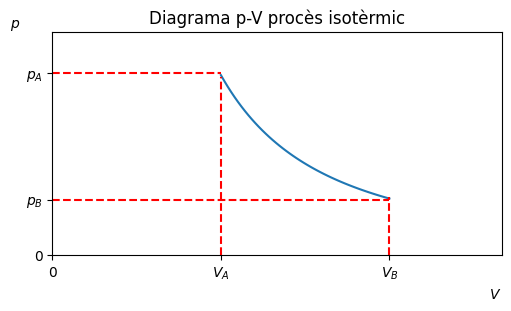
Procès adiabàtic#
També anomanat isoentropic, ja que l’entropia és constant. Aïllat tèrmicament, \(Q=0\)
Es defineix \(\gamma\) com el índex adiabàtic del gas, \(\gamma = \frac{c_P}{c_V}\)
Per a quest procés es compleix \(p_AV_A^\gamma = p_BV_B^\gamma\) i que \(T_AV_A^{\gamma-1} = T_BV_B^{\gamma-1}\)
\(W = \frac{1}{1-\gamma}p_BV_B-p_AV_A\)
\(Q = 0\)
\(W = -\Delta U = nC_V(T_B-T_A)\)
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
V=np.linspace(0.75, 1.5, 50)
gamma=5/3 #gas ideal monoatòmic
p=1/V**gamma
fig, ax = plt.subplots(1, 1, figsize=(5, 3), layout='constrained')
plt.plot(V, p)
plt.axhline(y=1.63, xmin=0, xmax=0.375, color='red',linestyle='--')
plt.axhline(y=0.5, xmin=0, xmax=0.75, color='red',linestyle='--')
plt.axvline(x=0.75, ymin=0, ymax=0.8, color='red',linestyle='--')
plt.axvline(x=1.5, ymin=0, ymax=0.26, color='red',linestyle='--')
ax.axis([0, 2, 0, 2])
ax.set_xticks([0,0.75,1.5], ['0','$V_A$','$V_B$'])
ax.set_yticks([0,1.63,0.5], ['0','$p_A$','$p_B$'])
ax.set_title('Diagrama p-V procès isotèrmic')
plt.xlabel('$V$', loc='right')
plt.ylabel('$p$', loc='top', rotation='horizontal')
plt.show()
Resum dels resultats per a cada transformació#
Transformació |
Característica |
Calor |
Treball |
Variació d’energia interna |
|---|---|---|---|---|
Isocora |
\(V=ct\) |
\(Q=nC_V(T_B-T_A)\) |
\(W=0\) |
\(\Delta U =nC_V(T_B-T_A)\) |
Isobara |
\(p=ct\) |
\(Q=nC_P(T_B-T_A)\) |
\(W=p(V_B-V_A)\) |
\(\Delta U =nC_V(T_B-T_A)\) |
Isoterma |
\(T=ct\) |
\(Q=W\) |
\(W=nRTln{\frac{V_B}{V_A}}\) |
\(\Delta U =0\) |
Adiabàtica |
\(Q=0\); \(S = ct\) |
\(Q=0\) |
\(W=-\Delta U\) |
\(\Delta U =nC_V(T_B-T_A)\) |